Номинальная и эффективная процентные ставки

ПРОЦЕНТНАЯ СТАВКА. БУДУЩАЯ СТОИМОСТЬ ДЕНЕГ

Вся финансовая математика базируется на предположении, что деньги со временем изменяют свою стоимость. Поэтому финансовую математику называют еще теорией стоимости денег во времени (Time Value of Money - TVM). Обладатель денег может инвестировать их в различные проекты с целью получения дохода в будущем. Очевидно, что инвестор ожидает получить сумму, превосходящую его вложения, то есть предполагает, что деньги будут расти со временем.

Одним из способов получения дохода с определенной суммы денег является помещение этой суммы на банковский счет. В данном случае владелец денег выступает как кредитор. Пусть сумма, вложенная в банк, равна PV. Тогда через год у владельца этих денег на счете будет сумма

FV = PV * (1 + i) (1),

где i - процентная ставка банка. Здесь мы использовали следующие общепринятые обозначения:
PV (Present Value) - сумма, которой владелец обладает сегодня, дословно - современная стоимость денег;
FV (Future Value) - сумма, которую получит владелец спустя определенное время; дословно - будущая стоимость денег.

К примеру, если банковская процентная ставка равна 10%, то через год сумма на счете вырастет в 1.1 раза. Доход кредитора составит:

i * PV = 0.1 * PV.

Существует два способа начисления процентов: по простой процентной ставке и по сложной. При начислении дохода по простой процентной ставке доход каждый раз начисляется на первоначально вложенную сумму.

То есть через год доход составит i * PV,

через два года - 2 * i * PV,

через 5 лет - 5 * i * PV,

через n лет - n * i * PV.

Таким образом, при начислении дохода по простой процентной ставке, через n лет на счете у владельца будет сумма

FV = PV * (1 + i * n) (2).

Если со времени первоначального вложения денег прошло время t, не равное целому числу лет, то вместо (2) можно написать:

FV = PV * (1 + i * t) (3),

где время t измеряется в годах.

 

Соотношение (3) описывает линейную зависимость будущей стоимости денег FV от времени t. Таким образом, при начислении дохода по простой процентной ставке деньги со временем растут по линейному закону.

Другим способом начисления дохода является использование сложных процентных ставок. При начислении дохода по сложной процентной ставке, доход начисляется не на первоначальную сумму, а уже на накопленную сумму.

То есть если

в конце первого года сумма на счете составляла PV * (1 + i),

то в конце второго года она составит PV * (1 + i * t)²,

в конце третьего года - PV * (1 + i * t)³ и т.д.

По прошествии n лет сумма на счете владельца составит

FV = PV * (1 + i)ⁿ (4),

Коэффициент (1 + i)ⁿ (5),

входящий в правую сторону последнего соотношения, называется коэффициентом наращения.

В общем случае, если со времени первоначального вложения денег прошло t лет (где t не обязательно целое число лет), то будущая стоимость денег составит

FV = PV * (1 + i)^t (6).

Мы видим, что при начислении дохода по сложной процентной ставке, деньги со временем растут по степенному закону.

Посмотрим, как изменяются деньги со временем при начислении дохода по одинаковым простой и сложной процентной ставкам. Сравнение формул (3) и (6) показывает, что в первый год деньги растут быстрее, если доход начисляется по простой процентной ставке. К концу первого года доходы, полученные по обеим ставкам, одинаковы. В дальнейшем деньги растут быстрее (причем, существенно), если начисление дохода происходит по сложной процентной ставке.

Пример 1. 1.000 рублей помещается в банк под 10% годовых. Определить стоимость вклада через 10 лет, если проценты начисляются а) по простой ставке, б) по сложной ставке.

Решение:
а) При начислении дохода по простой ставке будущая сумма будет

FV = 1000 * (1 + 10 * 0.1) = 2.000 руб.
б) В случае сложных процентных ставок
FV = 1000 * (1 + 0.1) * 10 = 2593.74 руб.

НОМИНАЛЬНАЯ И ЭФФЕКТИВНАЯ ПРОЦЕНТНЫЕ СТАВКИ

До сих пор мы рассматривали случай, когда процентная ставка начисляется один раз в году. Напомним, что величина 1 + i показывает, во сколько раз выросла сумма за один год. Такая процентная ставка называется эффективной (в дальнейшем эффективную процентную ставку будем обозначать буквой i).

В действительности, проценты могут начисляться несколько раз в году, например, ежеквартально (четыре раза в году), ежемесячно (12 раз в году), ежедневно (365 раз в году) и т.д. В этом случае мы имеем дело со сложной номинальной процентной ставкой j. Если указывается номинальная процентная ставка j, то всегда еще указывается, сколько раз в году происходит начисление процентов.

Рассмотрим пример, когда проценты начисляются ежемесячно. Тогда через месяц на счете у владельца будет сумма

.

В течение следующего месяца проценты начисляются на эту сумму, поэтому в конце второго месяца сумма на счете составит

2

через три месяца

3

и т.д. Таким образом, через год сумма на счете составит

(7).

С другой стороны, если эффективная процентная ставка i, то последнее соотношение можно записать как

FV = PV * (1 + i) (8).

Приравнивая (7) и (8), получаем связь между эффективной и номинальной процентными ставками (при начислении процентов 12 раз в году)

(9).

Обобщая, можно утверждать, что если номинальная ставка j начисляется m раз в году, то в конце первого года сумма на счете составит

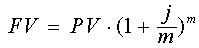(10).

Эффективная процентная ставка, при этом:

(11).

Соотношение (11) устанавливает связь между эффективной и номинальной ставками процента.