памяти компьютера (1 час)
Цель лекции: Рассмотреть логические элементы компьютера: логический вентиль, счетчики, регистры, триггеры; дать представление о данных в памяти компьютера; систем счисления; перевод из одной системы счисления в другую; представление звуковой и текстовой информации.
Вопросы лекции:
1. Логический вентиль
2. Триггеры
3. Счетчики
4. Регистры
5. Представление данных в памяти компьютера. Двоичные числа
6. Шестнадцатеричные числа
7. Представление текстовой информации
8. Представление звуковой информации
9. Системы счисления и действия в них: обратный, дополнительный код.
Содержание лекции:
Логический вентиль
Рассматриваются основные теоретические (математические, логические) понятия и сведения, касающиеся базовых логических элементов и структур – логических вентилей, логических (переключательных) схем, логической базы аппаратуры ЭВМ и их оптимальной структуры, оптимизации их структур.
Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.
Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.
Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.
Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).
Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.
Логическая функция "инверсия", или отрицание, реализуется логической схемой (вентилем), называемой инвертор.
Принцип его работы можно условно описать следующим образом: если, например, "0" или "ложь" отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или "истина", которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.
Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт ("истина"), то на выходе инвертора будет сниматься 0 вольт, то есть "ложь" (схемы на рисунках 1 а, б).

Рисунок 1. Принцип работы инвертора
Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рисунок 2), в которой замкнутая цепь соответствует 1 ("истина") или х = 1, а размыкание цепи соответствует 0 ("ложь") или х = 0.

Рисунок 2. Электрический аналог схемы инвертора
Дизъюнкцию  реализует логическое устройство (вентиль) называемое дизьюнктор (рисунок 3 а, б, в):
реализует логическое устройство (вентиль) называемое дизьюнктор (рисунок 3 а, б, в):

Рисунок 3 a

Рисунок 3 b
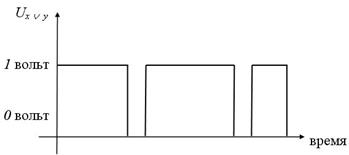
Рисунок 3 в Принцип работы дизъюнктора
Дизъюнктор условно изображается схематически электрической цепью вида (рисунок 4)

Рисунок 4 Электрический аналог схемы дизъюнктора
Конъюнкцию 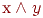 реализует логическая схема (вентиль), называемая конъюнктором (рисунок 5а, б, в):
реализует логическая схема (вентиль), называемая конъюнктором (рисунок 5а, б, в):

Рисунок 5а.

Рисунок 5б

Рисунок 5в. Принцип работы конъюнктора
Конъюнктор можно условно изобразить схематически электрической цепью вида (рисунок 6)

Рисунок 6. Электрический аналог схемы конъюнктора
Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рисунок 7 а, б, в). Есть и другие общепринятые формы условных обозначений.

Рисунок 7 а, б, в. Условные обозначения вентилей (вариант)
Пример. Транзисторные схемы, соответствующие логическим схемам  (инвертор),
(инвертор),  (дизъюнктор),
(дизъюнктор),  (конъюнктор) имеют, например, следующий вид (рисунок 8а, б, в):
(конъюнктор) имеют, например, следующий вид (рисунок 8а, б, в):

Рисунок 8a. Инвертор

Рисунок 8б. Дизъюнктор

Рисунок 8в. Конъюнктор
Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно "соединять" и "вкладывать" друг в друга (осуществлять композицию и суперпозицию схем).
Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные
Триггеры
Триггер – это логическая схема с положительной обратной связью, могущая неограниченно долго находиться в одном из двух устойчивых состояний (0 и 1) которые обеспечиваются положительной обратной связью, а не входным сигналом. Триггер скачком, лавинообразно меняет одно состояние на другое под воздействием входного сигнала.
Триггеры делятся на симметричные и несимметричные (триггеры Шмитта). Триггеры Шмитта рассматриваются как импульсные устройства, а симметричные делятся:
1. По способу записи информации на:
а) асинхронные,
б) синхронные (тактируемые).
2. По способу управления записью информации на:
а) статические,
б) динамические – по фронту переднему или заднему,
в) двухступенчатые – по двум фронтам.
3. По способу организации логической связи:
а) элементарные с раздельной установкой 0 и 1 – RS–триггеры
б) с приемом информации по одному входу – D–триггеры
в) со счетным входом – T–триггеры
г) универсальные с раздельной установкой 0 и 1 – JK–триггеры
д) комбинированные (смешанные)
Счетчики
На базе счетных триггеров можно построить цифровое устройство, получившее название электронного счетчика. Электронные счетчики (далее, просто счетчики) позволяют вести подсчет электрических импульсов, количество которых (поступивших на вход счетчика) представляется, обычно, в параллельном коде. Счетчики могут отличаться модулем счета и типом счетной последовательности, которая, в частности, может быть двоичной, двоично-десятичной, в коде Грея и т.п. Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты. Таким образом, любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Так как счетчики и делители имеют единую структуру, основное внимание будет уделено синтезу счетчиков.
Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.
Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.
Счетчики, независимо от способа синхронизации, подразделяются на счетчики прямого счета (суммирующие) и на счетчики обратного счета (вычитающие). В интегральном исполнении выпускаются также реверсивные счетчики, в которых имеется специальный вход для переключения режима работы, т.е. направления счета. Многие типы счетчиков, выпускаемые промышленностью в интегральном исполнении, имеют дополнительные входы предустановки, позволяющие использовать эти счетчики в режиме регистра памяти.
В качестве разрядных триггеров счетчиков и делителей могут быть использованы двухступенчатые D-триггеры, Т- и JK-триггеры.
Счетчики относятся к последовательностным устройствам с циклически повторяющейся последовательностью состояний. Число, соответствующее количеству импульсов (поступивших на вход счетчика), при котором счетчик “возвращается” в исходное состояние, называется модулем или коэффициентом счета. Модуль счета, обычно, обозначают буквой М (или Ксч). Например, максимальный модуль счета счетчика из двух триггеров равен М = 22 = 4, трех триггеров - М = 23 = 8 и т.д. В общем случае для n - разрядного счетчика - М = 2n. Модуль счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 позволяет реализовать (без дополнительных схемных затрат) делитель частоты на 8. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.
Регистры
Назначение регистров - хранение и преобразование многоразрядных чисел. Регистры обладают большими функциональными возможностями. Они используются в качестве управляющих и запоминающих устройств генераторов и преобразователей кодов, счетчиков, делителей частоты, узлов временной задержки.
Элементами структуры регистров являются синхронные триггеры D, RS или JK - типа с динамическим или статическим управлением. Так как одиночный триггер может запомнить один разряд (бит) двоичной информации, то его можно считать одноразрядным регистром. Для запоминания многоразрядных чисел используют "линейки " из нескольких триггеров - по количеству разрядов чисел. В схемы регистров входят также комбинационные элементы, роль которых в данном случае вспомогательная.
Занесение информации в регистр называют операцией ввода или считывания. Запись информации в регистр не требует его предварительного обнуления (сброса).
Все регистры в зависимости от функциональных свойств подразделяются на две категории: накопительные регистры (памяти, хранения) и сдвиговые.
В свою очередь сдвиговые регистры делятся: по способу ввода и вывода информации - на параллельные, последовательные и комбинированные (параллельно-последовательные и последовательно-параллельные); по направлению передачи (сдвига) информации - на однонаправленные и реверсивные.






