Турист, собираясь лететь на самолете, берет с собой багаж, вместимостью b кг, и собирает набор из 5 неделимых вещей.
Каждая вещь обладает весом ai и стоимостью сj
Составить такой набор вещей, который не превышает вместимость чемодана по весу, и будет обладать максимальной стоимостью.
| № варианта | c1 | c2 | c3 | c4 | c5 | b |
| a1 | a2 | a3 | a4 | a5 | ||
Задача №4. Корреляционно-регрессионный анализ
Для заданного варианта данных:
а) построить в Excel график зависимости х и у и определить вид зависимости.
б) Найти параметры зависимости, используя в Excel Поиск решения.
в) Подтвердить параметры зависимости, используя Линию тренда, вывести коэффициент детерминации и дать оценку качества регрессионной модели
г) Вычислить коэффициент корреляции х и у (функция Excel КОРРЕЛ) и дать оценку наличия и тесноты линейной связи
е) Выполнить прогноз значения у для любого нового значения х.
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Примечание. Для выбора вида эмпирической формулы зависимости использовать предложенные графики функций:
a) y=ax+b (линейная зависимость)
A>0 a<0


2) y=ax2+bx+c (квадратичная зависимость)
A>0 a<0


3) y=a/x+b (гиперболическая зависимость)
A>0 a<0


4) y=aex+b (показательная зависимость)
A>0 a<0


5) y=a*lnx+b (логарифмическая зависимость)
A>0 a<0
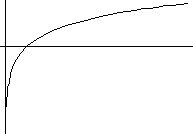

6) 
A>0 a<0


7) y=a*sinx + b*cosx + c

8) y=a*x+ b*sinx+c*cosx
A>0 a<0


9) y=a*arctgx +b
A>0 a<0


10) y=a*x2/(x2+1)+b
A>0 a<0


Синтаксис написания в Excel наиболее часто используемых математических функций приведен в таблице 1.
Таблица 1
| Математическая запись функции | Синтаксис функции в Excel |
| p | ПИ() (возвращает 3,14159286) |
| sin x | SIN(число) |
| cos x | COS(число) |
| tg x | TAN(число) |
| ctg x | 1/ TAN(число) |
| arcsin x | ASIN(число) |
| arccos x | ACOS(число) |
| arctg x | ATAN(число) |
| arcctg x = p/2 – arctg x | ПИ()/2 - ATAN(число) |
| |x| | ABS(число) |

| КОРЕНЬ (число) |

| x^(1/n) |
| xn | x^n или СТЕПЕНЬ(число; n) |
| ex | EXP(число) |
| Ln x | LN(число) |
| Lg x | LOG10(число) |
| Lognx | LOG(число; n) |
Пример задачи для письменного решения на
ЭКЗАМЕНЕ
по дисциплине
«Эконометрика и экономико-математические методы и модели»
По специальности «Финансы и кредит», 2 курс
Задача динамического программирования
1. Методом динамического программирования решить предложенную задачу.
2. Описать физический смысл каждого шага решения задачи.
3. Указать оптимальное решение задачи (оптимальный план распределения финансов и оптимальное значение целевой функции).
Оптимальное распределение средств на расширение производства.
Группе из 4-х (n=4) предприятий выделяются дополнительные средства на реконструкцию и модернизацию производства в размере A=100. По каждому из n предприятий известен возможный прирост gi(x) выпуска продукции в зависимости от выделенной ему суммы x.
Требуется так распределить между предприятиями средства C, чтобы общий прирост Fn(C) выпуска продукции был максимальным. Средства могут выделяться порциями 20, 40, 60, 80, 100.
| Вариант 1 | Вариант 2 | |||||||||
| С | g1(x) | g2(x) | g3(x) | g4(x) | С | g1(x) | g2(x) | g3(x) | g4(x) | |
| Вариант 3 | Вариант 4 | |||||||||
| С | g1(x) | g2(x) | g3(x) | g4(x) | С | g1(x) | g2(x) | g3(x) | g4(x) | |
| Вариант 5 | Вариант 6 | |||||||||
| С | g1(x) | g2(x) | g3(x) | g4(x) | С | g1(x) | g2(x) | g3(x) | g4(x) | |
| Вариант 7 | Вариант 8 | |||||||||
| С | g1(x) | g2(x) | g3(x) | g4(x) | С | g1(x) | g2(x) | g3(x) | g4(x) | |
| Вариант 9 | Вариант 10 | |||||||||
| С | g1(x) | g2(x) | g3(x) | g4(x) | С | g1(x) | g2(x) | g3(x) | g4(x) | |
Вопросы к экзамену по курсу
«Эконометрика и экономико-математические методы и модели»
1. Содержание экономико-математических моделей и методика их построения.
2. Информационное и математическое обеспечение экономико-математических моделей.
3. Общая классификация экономико-математических моделей.
4. Основные типы линейных экономико-математических моделей.
5. Система ограничений в экономико-математических моделях.
6. Понятие критерия оптимальности в экономико-математических моделях.
7. Общий вид задачи линейного программирования. Понятие целевой функции, ограничений, граничных условий.
8. Формирование экономико-математической модели задачи определения оптимального производственного плана предприятия.
9. Симплекс-метод решения задач линейного программирования.
10. Алгоритм решения задачи линейного программирования в Excel.
11. Модель оптимального раскроя промышленных материалов.
12. Сущность метода динамического программирования. Формулы Беллмана.
13. Решение задач целочисленного программирования методом ветвей и границ.
14. Решение задач о кратчайшем пути.
15. Экономико-математическая модель межотраслевого баланса.
16. Методы и модели теории игр.
17. Экономико-математические методы и модели теории игр.
18. Основные понятия сетевого планирования и управления. Правила построения сетевых графиков.
19. Математические методы сетевого планирования и управления.
20. Модели оптимального использования производственных мощностей. Максимизация объема производства изделий. Минимизация остатков незавершенного производства.
21. Регрессионный анализ и прогнозирование хозяйственной деятельности.
22. Простая и множественная регрессия.
23. Понятие аппроксимации зависимостей.
24. Сущность метода наименьших квадратов. Графическая интерпретация метода наименьших квадратов.
25. Виды линейных и нелинейных моделей с двумя параметрами для аппроксимации зависимостей.
26. Использование Excel для построения уравнения регрессии. Встроенные в Excel функции для аппроксимации значений.
27. Линейная модель множественной регрессии. Методы построения уравнения множественной регрессии.
28. Способы выбора вида модели регрессии. Какие функции чаще всего используются для построения уравнения парной регрессии.
29. Экономический смысл параметров уравнения линейной парной регрессии.
30. Проверка общего качества уравнения регрессии: стандартная ошибка оценки Y.
31. Проверка общего качества уравнения регрессии: коэффициент детерминации R2.
32. Оценка значимости уравнения регрессии: F-критерий Фишера.
33. Расчет линейного коэффициента парной корреляции xy R.
34. Построение доверительного интервала для линейного коэффициента парной корреляции.
35. Проверка статистической значимости коэффициентов уравнения регрессии: ковариационная матрица оценок.
36. Проверка статистической значимости коэффициентов уравнения регрессии: t –статистика Стьюдента.
37. Построение доверительного интервала прогноза в случае линейной регрессии.
38. Точечный прогноз по уравнению линейной регрессии.
39. Интервальный прогноз по уравнению линейной регрессии.
40. Расчет коэффициента эластичности Э, среднего коэффициента эластичности  .
.
41. Стандартизованные коэффициенты регрессии.
42. Понятия гомоскедастичности и гетероскедастичности. Проверка остатков на гомоскедастичность.
43. Нелинейные модели регрессии и их линеаризация.
44. Модели временных рядов.
45. Группы методов исключения тенденции.
46. Автокорреляция в остатках. Критерий Дарбина-Уотсона. Оценка параметров уравнения регрессии при наличии автокорреляции в остатках.
47. Модель распределенного лага.
48. Динамические распределенные модели.
49. Метод максимального правдоподобия: функция правдоподобия, уравнение правдоподобия.
50. Виды систем эконометрических уравнений.






