Кнопкою «Пуск води» запустите процес заповнення напірного бака і прозорої горизонтальної труби водою. Після наповнення бака до верхнього рівня переливної воронки, приступайте до відкриття головного вентиля. Управляти вентилем можна як безпосередньо одиночними клацаннями лівою кнопкою миші, так і клавішею клавіатури із стрілкою «вправо». Управляючи ступенем відкриття вентиля, ви зможете тільки збільшувати швидкість протікання води. По технічних причинах демонстраційного ролика зменшувати потік в цій лабораторній роботі не можна. Якщо необхідно буде повернутися до меншої швидкості перебігу води, доведеться скористатися кнопкою «скидання», повторити процес наповнення бака водою і знов встановити потрібну швидкість.
Для візуалізації режиму течії в трубі необхідно відкрити вентиль, що перекриває фарбувальну рідину, для чого досить кликнути по ньому лівою кнопкою миші. Цей вентиль відкриється тільки в тому випадку, якщо головний вентиль буде відкритий хоч би на одне ділення.
Віртуальна лабораторна установка для дослідження режиму руху рідини зображена на рис. 1.21. 
Рис. 1.21. Початковий стан віртуальної лабораторної роботи №7
Відкривши вентиль фарбувальної рідини, можна буде спостерігати режим руху рідини в прозорій горизонтальній трубі. Залежно від ступеня відкриття головного вентиля можна буде спостерігати спочатку ламінарний потік рідини, який поступово переходитиме в турбулентний. При цьому ламінарним режимом потрібно вважати тільки той, при якому струмінь фарбувальної рідини в загальному потоці абсолютно не спотворюється, а турбулентним — той, при якому струмінь фарби повністю розмивається, без залишку.
Для вимірювання швидкості потоку досить кликнути лівою кнопкою миші по спусковому клапану, після чого випорожниться мірна посудина і автоматично запуститься віртуальний таймер.
При цьому користуватися будь-яким іншим таймером забороняється, бо швидкість відтворення ролика безпосередньо залежить від швидкодії конкретного комп'ютера і може дуже відрізнятися від реальної. Як тільки в мірній посудині набереться достатня кількість води, зупиніть таймер і занесіть в таблицю 2.7 виміряний об'єм води і час таймера. Крім того, в таблицю необхідно також внести температуру води і діаметр прозорої горизонтальної труби.
Вимірювання повторюють як мінімум для двох режимів — ламінарного і турбулентного.
Далі переходьте до обчислень і заповніть необхідні елементи зведеної таблиці.
Лабораторна робота №1.8
«Визначення залежності між гідравлічним ухилом і середньою швидкістю при турбулентному русі води»
Мета роботи:
1. Визначення режиму руху (розрахунок числа Рейнольдса).
2. Встановлення залежності гідравлічного ухилу від швидкості:
а) побудова графічної залежності lgі=f(lgv);
б) визначення коефіцієнтів т і b аналітично і графічно.
3. Побудова графічної залежності lgl =f(lgRe).
Теоретична частина
Падіння повної питомої енергії потоку, віднесене до одиниці його довжини, називається гідравлічним ухилом для труб постійного перетину:
і=hдл/l (1.43)
Втрати напору по довжині потоку можуть істотно залежати від характеристики шорсткості стінок труби. Як відомо, при турбулентному режимі, безпосередньо примикаючи до стінки, розташований тонкий шар, рух в якому близько до ламінарного. Цей пристінний шар умовно називають ламінарним підшаром або плівкою. При турбулентному русі залежно від того, як співвідносяться розміри виступів шорсткості D і товщина ламінарної плівки, всі труби підрозділяються на три види.
Гідравлічно гладкою трубою називають таку, в якій висота виступів шорсткості стінки виявляється менше товщини ламінарного підшару (D<σ). В цьому випадку шорсткість стінок не впливає на характер руху, оскільки всі нерівності повністю занурені в ламінарну плівку. Отже, і втрати напору не залежать від шорсткості.
Якщо висота виступів шорсткості перевищує товщину ламінарного підшару (D>σ), труби називаються гідравлічно шорсткими. Турбулентний потік обтікає виступи з інтенсивним перемішуванням, що збільшує втрати напору.
Третій випадок є проміжним (D≈σ).
Товщина ламінарного шару визначається по формулі:
(1.44)
Отже, при русі потоку вздовж стінки з однаковою висотою виступів товщина ламінарної плівки міняється залежно від середньої швидкості (числа Рейнольдса).
Втрати напору по довжині визначаються по формулі Дарсі-Вейсбаха:
(1.45)
Ця формула дійсна як для ламінарного, так і для турбулентного режиму.
При ламінарному русі в трубах коефіцієнт Дарсі l залежить тільки від числа Рейнольдса і для круглих труб рівний:
l=64/ Re
Для інших видів поперечного перетину змінюється лише числовий коефіцієнт в чисельнику.
Підставивши значення l у формулу (1.45) і об'єднавши всі постійні величини в один коефіцієнт а, отримаємо рівняння Пуазейля:
(1.46)
де а — коефіцієнт, залежний від геометричних розмірів потоку і фізичних властивостей рідини.
При турбулентному режимі коефіцієнт Дарсі може залежати як від числа Рейнольдса, так і від відносної шорсткості ε = D /d. Іноді використовується зворотна величина, звана відносною гладкістю ε' = d/D.
В області гідравлічно гладких труб коефіцієнт Дарсі розраховується по формулі Блазіуса:
,
яка дає достовірні результати при Re < 100000. Підставляючи значення lгл в рівняння (2.45), отримаємо:
Коефіцієнт Дарсі в області гідравлічно шорстких труб (область квадратичного опору або квадратична область) залежить тільки від відносної шорсткості і не залежить від числа Рейнольдса (від середньої швидкості). Втрати по довжині в квадратичній області опору:
Звідси можна зробити висновок, що при турбулентному русі путні втрати розраховуються по загальній формулі:
(1.47)
де
b — коефіцієнт пропорційності, що враховує форму, довжину потоку і фізичні властивості рідини;
т — показник ступеня, міняється від 1,75 до 2,0 і залежить від гідравлічної шорсткості трубопроводу.
Для розрахунку гідравлічного ухилу рівняння (1.46) і (1.47) приймають вигляд:
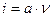і 
(1.48)
Коефіцієнти пропорційності а і b мають розмірності. Приведені рівняння справедливі для рівномірних потоків, тобто для сталих потоків з постійним живим перетином по всій довжині.
Порядок проведення роботи
Робота проводиться на установці, схематично зображеній на рис. 1.22.
Рис. 1.22. Схематичне зображення установки
Вода з напірного бака 1 при постійному напорі поступає в прямий трубопровід 2 діаметром 16 мм, завдовжки 650 мм, на початку і кінці якого встановлені п'єзометри 3 і 4.
Визначення втрати напору по довжині трубопроводу знаходиться по різниці показників п'єзометрів на початку і в кінці труби. При русі води в горизонтальній трубі постійного діаметру швидкість її не міняється, і з рівняння Бернуллі:
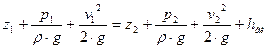
знаходимо:
Температуру води вимірюють і по таблиці 1.6 знаходять значення кінематичного коефіцієнта в'язкості.
Для знаходження залежності гідравлічного ухилу від швидкості проводять 6...8 дослідів, кожен з яких відрізняється величиною витрати. Для першого досліду встановлюють максимальну витрату води, вимірюють при цьому різницю показників п'єзометрів, потім витрата декілька зменшують прикриттям засувки на трубопроводі і повторюють вимірювання, які заносять в таблицю 1.8.
Таблиця 1.8
| № | hдл, м | V, м3 | t, с | t °С | u, м/с |
Обробка дослідних даних
Результати дослідів обробляють для отримання рівняння, що зв'язує гідравлічний ухил і середню швидкість потоку. Визначення швидкості потоку проводиться по витраті і площі живого перетину, м/с:
u= Q/S
причому витрату знаходять об'ємним методом по показанню лічильника 5 протікаючої води, м3/с:
Q = V/
Для встановлення режиму руху обчислюють число Рейнольдса:
Дослідні значення коефіцієнта Дарсі визначають з формули (2.45) після перетворення:
Розраховані значення числа Рейнольдса і коефіцієнта Дарсі використовують для побудови графіка lgl =f(lgRe).
Гідравлічний ухил обчислюють за формулою (1.43) і будують графік залежності lgі=f(lgv), відклавши по осі ординат значення lgі, а по осі абсцис — lgv. Логарифми ухилу і швидкості відкладаються на осях в однаковому масштабі. Отриманий на графіці ряд точок необхідно об'єднати однією прямою лінією так, щоб вона була середньою між ними.
Подальше завдання полягає у визначенні значень коефіцієнтів т і b рівняння (2.48). При логарифмуванні його виходить рівняння прямої лінії:
lgі=lgb + т•lgv. (1.49)
Значення коефіцієнтів необхідно визначити аналітичним і графічним методами.
У приведеному рівнянні (1.49): lgb — відстань від початку координат до точки перетину осі ординат з прямою; т — кутовий коефіцієнт, рівний тангенсу кута нахилу прямої до осі абсцис.
При аналітичному визначені коефіцієнтів вибирають на прямій (на графіку) довільні дві точки та знаходять їх координати. Записав координати для першої точки lgv1 и lgі1 для другої - lgv2, lgі 2, складають систему рівнянь з двома невідомими - lgb и т (рис. 2.41):
lgі1=lgb + т•lgv1
lgі2=lgb + т•lgv2
Вирішуючи рівняння, отримаємо:
;
lgb=lgі1-т•lgv1
Рис 2.41. Графік залежності lgі=f(lgv)
По величині lgb потенціюванням знайдемо значення коефіцієнта b.
Всі розрахункові величини поміщають в таблицю 1.9.
Таблиця 1.9
| № | Q, м3/с | v, м/с | lgv | i | lgi | Re | lgRe | lоп | lglоп |
