Глава 3. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ФИРМЫ
В РАЗЛИЧНЫХ РЫНОЧНЫХ УСЛОВИЯХ.
Типы рынков.
Отраслью называется группа фирм, производящих некоторый продукт или класс продуктов, которые в значительной степени способны замещать один другой, т.е. с относительно высокой перекрестной ценовой эластичностью спроса.
Конкуренты данного предприятия – это фирмы, на товар которых переключится его потребитель, если предприятие несколько (5-10%) повысит цену на свой товар.
Если отраслью выпускается стандартный продукт или продукты с высокой перекрестной ценовой эластичностью, будем говорить, что продукция отрасли является однородной, в противном случае – дифференцированной.
Классификация отраслей
| Товар | |||
| Однородный | Дифференцированный | ||
| Число продавцов | Один | Монополия | – |
| Мало | Олигополия | Дифференцированная олигополия | |
| Много | Чистая (совершенная) конкуренция | Монополистическая конкуренция |
Планирование производства в условиях совершенной конкуренции
Предположим, что фирма с данной функцией общих издержек, действует в условиях совершенной конкуренции. Рыночный спрос на продаваемый ею товар задан функцией x = x (p).
Будем считать, что конкуренция в отрасли является совершенной, если каждая фирма признает, что рыночная цена устанавливается не ею, не зависит от объема ее выпуска, и по этой цене она теоретически может продать любое (не превышающее величины рыночного спроса) количество продукции.
Предположим, что в рассматриваемый момент времени продажи в отрасли происходят по цене p. В этих условиях кривая спроса на продукцию фирмы выглядит следующим образом:

Рис. 1. Кривая спроса на продукцию фирмы в условиях совершенной конкуренции
Таким образом, выпустив x единиц продукции (закупив для продажи партию товара объемом в x единиц), фирма не продаст ни одной единицы товара по цене p¢ > p; по цене p продаст любое количество товара x Î [0, x p];
При цене p¢ < p все потребители продукции отрасли переключатся на товар, предлагаемый рассматриваемой фирмой, что даст ей возможность полностью обеспечить рыночный спрос, который составит x (p¢) единиц. Однако структура издержек фирм в отраслях, в которых складывается совершенная конкуренция такова, что продажа товаров в таких больших объемах может принести фирме разве лишь значительные убытки.
Таким образом, у фирмы нет оснований отклоняться от сложившейся в отрасли цены, и проблема планирования сводится к проблеме определения объема предложения товара, максимизирующего прибыль фирмы. При сделанных предположениях, выпустив x единиц товара и назначив на него цену p, она получит прибыль в размере 
Таким образом, планирование деятельности фирмы в условиях совершенной конкуренции может быть формализовано в виде следующей задачи математического программирования:
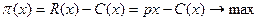 , ,  . .
| (*) |
Поскольку в условиях совершенной конкуренции фирме невыгодно пытаться удовлетворить весь рыночный спрос, решение задачи достигается во внутренней точке допустимого множества, то есть в критической точке функции прибыли. Выпишем производную этой функции и приравняем к 0:
 .
.
Необходимое условие максимальной прибыли совершенного конкурента: если максимум функции прибыли достигается в ее критической точке x *, то в этой точке выполняется соотношение  или
или  .
.
Функция x=s(p), сопоставляющая рыночной цене p объем предложения товара s(p), который принесет производителю наибольшую прибыль, называется функцией предложения фирмы.
Обозначим наименьшее значение функции средних переменных издержек на промежутке [0, x p ] через AVCmin (оно существует в силу нашего предположения о характере изменения средних издержек). Предположим, что оно достигается в точке x min.
Легко показать, что при p < AVCmin решение задачи (*) совпадает с левой границей допустимого множества – точкой x=0. Поскольку при x=0 прибыль продавца совпадает с его постоянными издержками, взятыми со знаком минус, это означает, что любое предложение товара приведет к убыткам, превосходящим постоянные издержки продавца.
Таким образом, при p < AVCmin продажа товара не имеет экономического смысла, т.е. x=0, или s(p)=0 (следует прекратить производство).
При p = AVCmin задача (*) имеет два решения: x=0 и x = xmin, поскольку
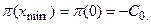
Экономически это означает, что при продаже x min единиц продукции доход продавца в точности покрывает его переменные издержки, и он терпит убытки в размере постоянных издержек. Отметим, что любое другое предложение приводит к еще большим убыткам. Цена на уровне минимальных средних переменных издержек называется ценой закрытия фирмы.
На практике выбор конкретной альтернативы из двух имеющихся в данном случае определяется прежде всего желанием фирмы быть представленной на рынке рассматриваемого товара.
Проанализируем величину прибыли, пользуясь равенством  .
.
Обозначим наименьшее значение функции средних общих издержек на промежутке [0, x p ] через ACmin. Предположим, что оно достигается в точке x 0.
Если  , рыночная цена выше себестоимости, то экономическая прибыль положительна.
, рыночная цена выше себестоимости, то экономическая прибыль положительна.
При рыночной цене p = ACmin доход, издержки и прибыль фирмы составят, соответственно,
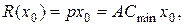


Цена товара, при которой доход продавца в точности совпадает с его издержками, называется ценой безубыточности.
Таким образом, при цене, равной минимальной себестоимости pбезуб = ACmin, фирма в точности может покрыть свои издержки, выставив на продажу x 0 единиц товара. При других объемах предложения она будет терпеть убытки.
AVCmin< p £ ACmin В этом случае прибыль отрицательна, фирма несет убытки. Но, следуя правилу  , фирма минимизирует убытки. Выручка от продажи x * единиц товара компенсирует полностью переменные издержки и часть постоянных. Это выгодней, чем остановить производство, ведь тогда убытки будут в размере постоянных издержек
, фирма минимизирует убытки. Выручка от продажи x * единиц товара компенсирует полностью переменные издержки и часть постоянных. Это выгодней, чем остановить производство, ведь тогда убытки будут в размере постоянных издержек  .
.
Определим объем предложения товара геометрически при p > AVCmin., исходя из необходимого условия max прибыли:  .
.
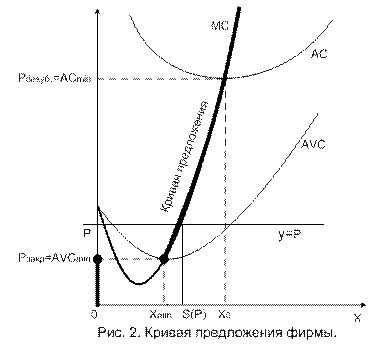
Графиком функции предложения в системе координат «предложение» – «цена» будет множество точек вида {(s (p), p), p ³ 0}. Изобразим в рассматриваемой системе координат кривую предельных издержек y = MC(x) и прямую y = p (рис.2).
Заметим, что прямая y = p может пересекать кривую предельных издержек в двух точках. Однако легко показать, что на промежутке убывания предельных издержек (C¢¢(x) < 0) функция прибыли фирмы выпукла:  и не может достигать максимума.
и не может достигать максимума.
Таким образом, при цене p прибыль фирмы будет максимальна в точке x = s (p), которая является абсциссой точки пересечения прямой y = p и возрастающей ветви кривой предельных издержек y = C¢(x). Полученная нами точка (s (p), p) графика функции предложения лежит на кривой предельных издержек. В связи с этим принято говорить, что при p ≥ AVCmin кривая предложения фирмы совпадает с возрастающей ветвью кривой предельных издержек. Вторая ветвь графика ниже точки закрытия фирмы (при p ≤ AVCmin) совпадает с вертикальной осью, где предложение х=0.
Аналитически функцию предложения можно найти, разрешив уравнение  относительно х* (пример см. [12]).
относительно х* (пример см. [12]).
Математическое моделирование поведения продавца в условиях монополии
Теперь рассмотрим противоположную рыночную структуру – монополию.
Монополия - это такая рыночная структура, когда одному производителю (продавцу) противостоит много покупателей. Модель монополии основана на следующих допущениях:
· отсутствие совершенных заменителей товара (перекрестная ценовая эластичность спроса между продукцией монополиста и любым другим товаром близка к нулю),
· отсутствие свободы входа на рынок (отрасль)
· совершенная информированность монополиста о кривой спроса на свою продукцию (его кривая спроса совпадает с кривой рыночного спроса).
Отметим принципиальную разницу между моделью поведения совершенного конкурента и несовершенного, в том числе монополиста, при внешней схожести формул. У совершенного конкурента кривая спроса на его продукцию горизонтальна, цена совпадает с предельной выручкой и со средней выручкой, доход растет пропорционально количеству проданного товара. А несовершенный конкурент сталкивается с понижающейся кривой спроса, поэтому предельная выручка ниже цены, и только при продаже первой единицы товара предельная выручка равна его цене. Графически кривые спроса и предельного дохода выходят из одной точки на оси Ор, далее кривая предельного дохода лежит ниже кривой спроса (рис. 3).
Предположим, что фирма намерена произвести x единиц товара и продать их по цене p. Назовем вектор (x, p) планом монополиста. Будем считать, что продавец в процессе планирования рассматривает любые сочетания объема выпуска товара и цены его продажи. Такое планирование называется долговременным.
Будем предполагать, что продавец выбирает план (x, p) таким образом, чтобы максимизировать свою прибыль.
Можно показать, что при долговременном планировании любой план (x, p), не принадлежащий кривой спроса, не может принести монополисту наибольшую прибыль. Таким образом, ему следует рассматривать только такие планы, при которых спрос совпадает с предложением. Переменные не являются независимыми, поэтому в качестве оптимизируемой переменной надо выбрать одну из них, удобнее x.
Предположим, что продавец решил закупить x единиц товара (x £ a). Весь товар будет реализован, если на него назначить цену в соответствии с законом спроса p=p(x). При этом выручка (доход) продавца составит R(x) = xp (x) денежных единиц, а прибыль, соответственно, p(x) = R(x) – C(x).
Таким образом, задача нахождения плана деятельности монопольного продавца, желающего получить в долговременном плане наибольшую прибыль, может быть формализована как следующая задача математического программирования:
| p(x)=R(x) – C(x)= xp (x) – C(x) ® max, x Î[0, a ], |
где a – объем спроса на товар при p =0.
Решение задачи заведомо существует (в силу теоремы Вейерштрасса) и искать его следует либо среди критических точек функции прибыли, либо на границе допустимого множества задачи: при x =0 или при x = a.
Заметим, что решение задачи не может совпадать с правой границей допустимого множества, поскольку такое количество товара можно реализовать только бесплатно, и будет справедливо следующее неравенство: p(a) = – C(a) < – C(0) = p(0).
Таким образом, для решения задачи достаточно найти критические точки функции прибыли p(x) из уравнения p¢(x)=0, вычислить значение прибыли продавца в этих точках и сравнить полученные результаты с его постоянными издержками.
Если есть основания считать, что в долговременном плане продавцу не имеет смысла покидать рассматриваемый рынок, решение поставленной задачи можно получить графическим способом. Сделанное предположение означает, что решение задачи отлично от x =0, и достигается в некоторой критической точке x * функции прибыли:
p¢(x *)=R¢(x *)–C¢(x *)=0.
Таким образом, продавец получит наибольшую прибыль при таком объеме предложения товара, при котором его предельный доход совпадет с предельными издержками. MR(x *)=MC(x *). Это равенство предельной выручки и предельных затрат называют необходимым условием оптимального плана. Выполнение условия максимума прибыли второго порядка в критической точке гарантирует, что эта найденная точка и есть оптимальный объем выпуска.
 Геометрически проиллюстрируем решение задачи нахождения оптимального плана монополиста. Изобразим графики полученных функций предельного дохода R¢(x) и предельных издержек C¢(x) вместе с графиком функции спроса p (x) в одной системе координат (рис. 3):
Геометрически проиллюстрируем решение задачи нахождения оптимального плана монополиста. Изобразим графики полученных функций предельного дохода R¢(x) и предельных издержек C¢(x) вместе с графиком функции спроса p (x) в одной системе координат (рис. 3):
При сделанных предположениях абсцисса точки пересечения кривой предельного дохода с кривой предельных издержек является точкой максимума прибыли, оптимальным объемом предложения x *. Найдя эту точку, можно, используя кривую спроса, определить цену товара р *, при которой спрос совпадет с предложением. Точка (x *, р *) на кривой спроса есть оптимальный план монополиста.
Поскольку в реальной экономической ситуации принцип максимизации прибыли редко реализуется в чистом виде, полезно знать, при каком объеме предложения доход продавца превышает его издержки и наоборот.
Точки x 1 и x 2 (объемы предложения, при которых доход продавца в точности равен его общим издержкам) называются точками безубыточности. Для их аналитического нахождения достаточно решить следующее уравнение:
R(x) = C(x).
Графически найдем точки безубыточности. Для этого построим (рис.4) в одной системе координат графики функций дохода R(x) и общих издержекC(x), абсциссы их точек пересечения есть те самые объемы выпуска (предложения), при которых доходы совпадают с издержками.

Рис. 4. Анализ прибыльности с помощью точек безубыточности
Таким образом, предложение товара в размере от x 1 до x 2 единиц товара позволит получить фирме положительную прибыль, иное предложение приведет к убыткам.
Свяжем предельный доход с эластичностью спроса:
MR=R¢(p) = x (p) + px ¢(p) = x (p)[1+ ep (x)].
Выручка продавца достигает максимального значения при цене, когда MR=0, т.е. при обращении в 0 скобки 1+ ep (x)=0  ep (x) = -1, что означает нейтральный спрос. При этом соответствующий объем спроса точка хЕ - точка пересечения кривой предельного дохода с осью ОХ.
ep (x) = -1, что означает нейтральный спрос. При этом соответствующий объем спроса точка хЕ - точка пересечения кривой предельного дохода с осью ОХ.
При неэластичном спросе 1+ ep (x)<0 предельный доход отрицательный, а предельные затраты всегда положительны, поэтому необходимое условие максимальной прибыли просто невыполнимо. Следовательно, прибыль монополиста может быть максимальной лишь при эластичном спросе 1+ ep (x)>0 (e >1). В этом случае прибыль достигает своего наибольшего значения при меньшем объеме предложения, чем доход (на рис. 3 точка х* левее хЕ).
Дуополия Курно.
Олигополия – тип строения рынка строения рынка, при котором сторона предложения представлена:
- Небольшим числом сравнительно крупных предприятий
- Однородная продукция или близкие субституты
- Возможность входа варьирует в широких пределах
Особенность олигополии во всеобщей взаимозависимости поведения фирм. Олигополист не может знать кривую спроса на свой товар. Он должен сделать некоторые предположения о реакции своих соперников на принимаемые им решения об уровне цены и\или выпуска,
Не существует единой модели олигополии. Разные модели отличаются характером предположений олигополистов и особенностями их взаимоотношений.
Мы рассматриваем поведение некооперирующихся олигополистов, действующих на свой страх и риск независимо друг от друга.
Дуополия – частный случай олигополии, когда на рынке всего два производителя, каждый из которых максимизирует свою прибыль. Если в качестве управляемой переменной выбрать величину выпуска, то получим количественную модель дуополии (одна из них модель Курно), если же – цену, то получим ценовую модель олигополии (например, модель Бертрана). Надо учитывать, что прибыль каждого из них будет функцией не только собственного выпуска, но и выпуска соперника 
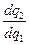 и
и 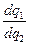 характеризуют реакцию второго (первого) дуополиста на решение о величине выпуска, принятое первым так, как она субъективно представляется первому (второму). Это предположительные вариации, или предположения субъектов количественной дуополии о вариациях (изменениях) выпуска соперника.
характеризуют реакцию второго (первого) дуополиста на решение о величине выпуска, принятое первым так, как она субъективно представляется первому (второму). Это предположительные вариации, или предположения субъектов количественной дуополии о вариациях (изменениях) выпуска соперника.
Модель Курно основана на предположении, что соперник не изменит свой выпуск в ответ на собственное решение первого дуополиста, т.е. выпуск другого задан. Предположительные вариации имеют нулевую оценку:

Рассмотрим простейшую модель дуополии Курно, когда соперники равны, их средние издержки постоянны и равны с, спрос на их продукцию линейный:
 - обратная функция рыночного спроса, где
- обратная функция рыночного спроса, где
 ,
,

Прибыли дуополистов: 

Из условия максимума прибыли выведем уравнения кривых реагирования дуополистов на величину выпуска, предложенного соперником (кривые наилучшего ответа).

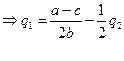


Этим уравнениям соответствуют линии на рис.5 – кривые наилучшего ответа или кривые реагирования 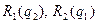 .
.
 Решив систему из этих двух уравнений, получим:
Решив систему из этих двух уравнений, получим: 

Точка пересечения кривых реагирования обоих дуополистов на одной плоскости (пространстве выпусков) определяет равновесие Курно. Равновесные выпуски являются координатами точки равновесия выпусков Курно-Нэша (точка C-N (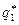 ,
,  )).
)).

 условие максимизации прибыли 2-го порядка выполняется и, следовательно, выпуски
условие максимизации прибыли 2-го порядка выполняется и, следовательно, выпуски 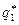 и
и  обеспечивают max
обеспечивают max  и
и  .
.
Рис.5. Равновесие Курно.
Найдем значение равновесной цены дуополии Курно:

Получили, равновесные выпуски и цены дуополистов Курно одинаковы, что объясняется однородностью продуктов и равенством затрат на производство. Равновесие Курно стабильно, если кривая реагирования первого имеет более крутой наклон, чем кривая второго. И тогда олигополия способна к самовосстановлению нарушенного какими-то внешними причинами равновесия.
Пример. Каждая из двух фирм владеет источником минеральной воды, который она может эксплуатировать с нулевыми затратами. Свою продукцию (минеральную воду) они продают на рынке, спрос на котором задан линейной функцией P = 100-2Q. Каждый дуополист исходит из предположения, что его соперник не изменит своего выпуска в ответ на его собственное решение. Дуополист руководствуется стремлением к максимизации своей прибыли, полагая выпуск другого заданным  . Сколько каждый из них будет выпускать воды и по какой цене?
. Сколько каждый из них будет выпускать воды и по какой цене?
► Прибыль одного дуополиста  , т.к. С=0. Учитывая, что
, т.к. С=0. Учитывая, что  , цена по закону спроса
, цена по закону спроса  .
.

Аналогично 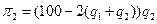
Условие max прибыли для первого дуополиста  ,
,
 для второго дуополиста. Отсюда
для второго дуополиста. Отсюда
 ,
,  - уравнения кривых реагирования дуополистов.
- уравнения кривых реагирования дуополистов.
Решив систему этих двух уравнений, получим равновесные выпуски:  ,
, 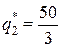
Общий выпуск составит  =
= 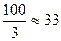 .
.
Равновесная цена продукции 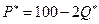 =
= 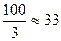 . Заметим, что монополист в этой отрасли выпускал бы 25 единиц продукции по цене 50 денежных единиц. ◄
. Заметим, что монополист в этой отрасли выпускал бы 25 единиц продукции по цене 50 денежных единиц. ◄






