М И Н И С Т Е Р С Т В О О Б Р А З О В А Н И Я Р О С С И Й С К О Й Ф Е Д Е Р А Ц И И
ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА
КАФЕДРА «ИНФОРМАТИКА»
АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ
ОСНОВЫ ЭВМ

ШАХТЫ 2000
АРИФМЕТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК
СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления — это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.
Все системы счисления можно разделить на два класса: позиционные и непозиционные. Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления. Ниже приведена табл. 1, содержащая наименования некоторых позиционных систем счисления и перечень знаков (цифр), из которых образуются в них числа.
Таблица 1
Некоторые системы счисления
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 | |
| Четвертичная | 0,1,2,3 | |
| Пятеричная | 0,1,2,3,4 | |
| Восьмеричная | 0,1,2,3,4,5,6,7 | |
| Десятичная | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9,A,B | |
| Шестнадцатеричная | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F |
В позиционной системе счисления число может быть представлено в виде суммы произведений коэффициентов на степени основания системы счисления:

(знак «точка» отделяет целую часть числа от дробной; знак «звездочка» здесь и ниже используется для обозначения операции умножения). Таким образом, значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Именно поэтому такие системы счисления называют позиционными.
Примеры (индекс внизу указывает основание системы счисления):
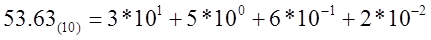
(в данном примере знак «3» в одном случае означает число единиц, а в другом - число сотых долей единицы);
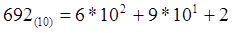
(«Шестьсот девяносто два» с формальной точки зрения представляется в виде «шесть умножить на десять в степени два, плюс девять умножить на десять в степени один, плюс два»).
Отметим, что кроме рассмотренных выше позиционных систем счисления существуют такие, в которых значение знака не зависит от того места, которое он занимает в числе. Такие системы счисления называются непозиционными. Наиболее известным примером непозиционной системы является римская. В этой системе используется 7 знаков (I, V, X, L, С, D, М), которые соответствуют следующим величинам:
| I(1) | V(5) | Х(10) | L(50) | С(100) | D(500) | М(1000) |
Примеры: III (три), LIX (пятьдесят девять), DLV (пятьсот пятьдесят пять).
Недостатком непозиционных систем, из-за которых они представляют лишь исторический интерес, является отсутствие формальных правил записи чисел и, соответственно, арифметических действий над ними (хотя по традиции римскими числами часто пользуются при нумерации глав в книгах, веков в истории и др.).






