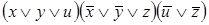Этап 1. Применим к исходной КНФ следующие действия: раскроем скобки; удалим дублирующие компоненты; удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание.
В результате, получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ.
Этап 2. В полученном на этапе 1 выражении удалим нулевые дизъюнктивные слагаемые.
Этап 3. В полученном на этапе 2 выражении: проведем все поглощения; удалим дублирующие компоненты.
В результате проведенных действий, получим сокращенную ДНФ функции f.
Рассмотрим пример построения сокращенной ДНФ с помощью метода Нельсона для функции f = (1111010010101111).
Построим для заданной функции КНФ:
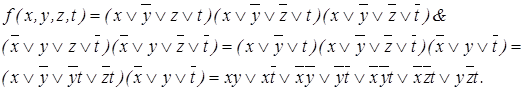
Сокращенная ДНФ для рассматриваемой функции примет вид: 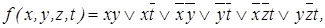
Рассмотрим также пример построения сокращенной ДНФ по следующей заданной КНФ: 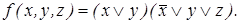
После раскрытия скобок, получим следующий результат:
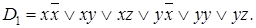
После второго этапа преобразований, получим сокращенную ДНФ:
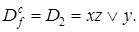
Следует отметить, что под тупиковой ДНФ (ТДНФ) переключательной функции f понимается такая ДНФ ее простых импликант, из которой нельзя выбросить ни одной импликанты, не изменив указанной функции.
Всякая минимальная ДНФ некоторой функции является тупиковой ДНФ, а именно: в МДНФ входят только простые импликанты (иначе некоторые множители в непростой имликанте можно было бы удалить, в противоречие с минимальностью исходной ДНФ); в МДНФ нет лишних импликант (иначе исходная ДНФ не являлась бы минимальной).
Таким образом, для получения МДНФ функции f достаточно построить все ТДНФ данной функции и выбрать из них те, которые содержат минимальное число букв.
3 КОНТРОЛЬНІ ПИТАННЯ
1. Сформулювати основнi концепції мінімізації перемикальних функцiй.
2. Виконати огляд проблеми мiнiмiзацiї перемикальних функцiй.
3. Пояснити особливостi технологiї мінімізації перемикальних функцій за допомогою методу Квайна
4. Навести та прокоментувати приклад мінімізації перемикальної функцій за допомогою методу Квайна.
5. Пояснити суть методу мiнiмiзацiї Квайна.
6. Сформулювати спiльнi та вiдмiннi властивостi методiв мiнiмiзацiї Квайна та Квайна-Мак-Класкi.
7. Охарактеризувати метод мiнiмiзацiї Блейка-Порецького.
8. Пояснити основний принцип знаходження покриттів перемикальних функцiй методом Петрика.
9. Охарактеризувати особливостi мiнiмiзацiї перемикальних функцiй iз застосуванням методу невизначених коефiцiєнтiв.
10. Сформулювати практичне призначення для мiнiмiзацiї перемикальних функцiй методу Нельсона.
4 ІНДИВІДУАЛЬНІ КОНТРОЛЬНІ ЗАВДАННЯ
ЗАВДАННЯ 1.
Мiнiмiзувати за допомогою методу Квайна аналiтичнi вирази перемикальних функцій, отриманi у процесi виконання лабораторної роботи 3. Побудувати для отриманих мінімальних нормальних форм перемикальних функцiй комбінаційні схеми, застосовуючи iнструментальне середовище відповідної спецiалiзованої програми (Electronics Workbench або т.i.).
ЗАВДАННЯ 2. Знайти за допомогою методу Квайна для одного з наведених нижче варiантiв перемикальних функцiй мiнiмальну диз`юнктивну та кон`юнктивну нормальну форму (МДНФ, МКНФ):
1) 
2) 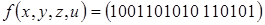
3) 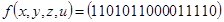
4) 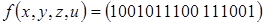
5) 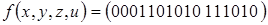
6) 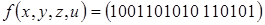
7) 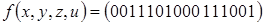
8) 
9) 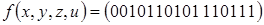
10) 
ЗАВДАННЯ 3. Знайти мiнiмальну диз`юнктивну нормальну форму (МДНФ) для того ж варiанту перемикальної функцiї, що й у завданнi 1, за допомогою методу Квайна-Мак-Класкi; порiвняти отриманi результати.
ЗАВДАННЯ 4. Знайти за допомогою методу Блейка-Порецького скорочену ДНФ перемикальної функции на основi її довiльної ДНФ для одного з наведених нижче варiантiв перемикальних функцiй:
1) 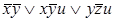
2) 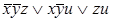
3) 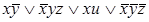
4) 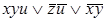
5) 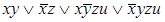
6) 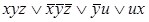
7) 
8) 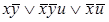
9) 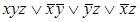
10) 
ЗАВДАННЯ 5. Знайти мiнiмальну диз`юнктивну нормальну форму (МДНФ) для одного з наведених нижче варiантiв перемикальних функцiй, застосувавши метод Петрика в якостi промiжного методу (для знаходження всiх минимальних покриттів конституент одиницi та отримання всiх тупикових ДНФ за iмплiкантною матрицею).


ЗАВДАННЯ 6.
Виконати мiнiмiзацiю перемикальної функцiї iз застосуванням методу невизначених коефіцієнтів і методу Нельсона. Побудувати вiдповiднi комбiнацiйнi схеми.
Варiанти перемикальних функцiй:
1) 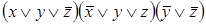
2) 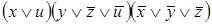
3) 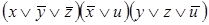
4) 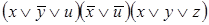
5) 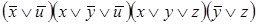
6) 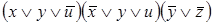
7) 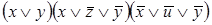
8) 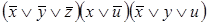
9) 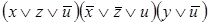
10)