ВНЕШНИЙ ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
Явление внешнего фотоэлектрического эффекта (фото-электронной эмиссии) состоит в испускании электронов веществом при воздействии на них световой энергии. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.
Явление внешнего фотоэффекта было исследовано А.Г. Столетовым в 1888 году. Оказалось, что: 1) при фиксированной частоте падающего света число фотоэлектронов, вырываемых с поверхности металла в еди-ницу времени, пропорционально интенсивности света; 2) величина мак-симальной скорости фотоэлектронов не зависит от интенсивности па-дающего света, а определяется лишь длиной его волны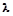 
(частотой ν): 
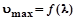; 3) каждому веществу свойственна длинноволновая (крас-ная) граница фотоэффекта 
, зависящая от химической природы вещества и состояния его поверхности. При 
фотоэффект не наблюдается.
С волновой точки зрения классическая физика эти особенности фотоэффекта не может объяснить. Полностью объясняет явление фотоэффекта лишь квантовая теория света, предложенная Эйнштейном в 1905 г. За открытие и объяснение законов фотоэффекта Эйнштейн в 1921 г. был удостоен Нобелевской премии по физике.
Современная квантовая теория рассматривает свет как поток отдельных частиц, называемых фотонами. Энергия фотона e зависит от частоты света n (длины волны l):
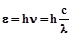, (2.1)
где h – постоянная Планка, c – скорость света в вакууме.
При фотоэффекте фотон, встречаясь со свободным электроном металла, отдает всю свою энергию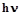 
этому электрону. Электрон, получив энергию фотона, затрачивает часть ее на преодоление потенциального барьера (работу выхода электрона из металла А), а оставшаяся часть идет на сообщение этому электрону кинетической энергии вне металла 
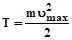. По закону сохранения энергии,
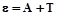, или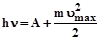 
. (2.2)
Это соотношение получило название уравнение Эйнштейна для внешнего фотоэффекта.
Из уравнения Эйнштейна видно, что скорость электрона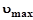 
, вырванного из металла в результате фотоэффекта (фотоэлектрона), зависит от частоты n (длины волны l) падающего света, так как величины h, m, A (для данного металла) постоянные. Следовательно, если 
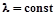то и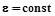 
, тогда
. (2.3)
Более того, скорость фотоэлектронов 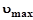не зависит от интенсивности I падающего света, поскольку интенсивность монохроматического (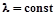) света определяется числом фотонов в пучке: 
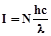. Если большее число фотонов N встречается со свободными электронами внутри металла, то будет больше вырванных фотоэлектронов, скорость же их не изменится.
Если энергия фотона такова, что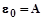 
, то, согласно уравнению Эйнштейна (2.2),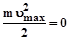 
и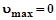 
. Следовательно, при осве-щении металла светом, длина волны которого 
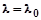, энергия фотона 
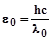достаточна лишь для того, чтобы совершить работу выхода А (удалить электрон из металла), но не достаточна для сообщения электрону скорости, когда он покинет металл. Длина волны 
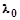называется красной границей фотоэффекта. Таким образом, при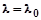
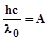. (2.4)
Это выражение представляет собой уравнение Эйнштейна для красной границы. Согласно выражению (2.4), красная граница фотоэффекта определяется по формуле
. (2.5)
Таким образом, красная граница фотоэффекта 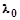, зависящая только от работы выхода электрона из металла А, различна для разных металлов (поскольку для разных металлов А различна).
Если длина волны света 
, то фотоэффект не наблюдается, так как в этом случае энергия кванта меньше работы выхода электрона (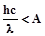
). Электрон обладает энергией, недостаточной для преодоления потенциального барьера, и остается внутри металла.
Таким образом, законы фотоэффекта свидетельствуют о следующем:
1) число вырванных фотоэлектронов пропорционально числу падающих фотонов (интенсивности света) при ;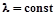
2) кинетическая энергия фотоэлектронов пропорциональна частоте n (длине волны λ) падающего света;
3) каждому веществу свойственна красная граница фотоэффекта (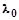
).
Фотоэффект безынерционен, то есть испускание фотоэлектронов начинается сразу же, как только на металл падает свет с длиной волны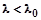 
. Это свойство внешнего фотоэффекта является ещё одним подтверждением квантового характера взаимодействия света с вещест-вом. Согласно же классическим волновым представлениям, требуется значительное время для того, чтобы электромагнитная волна заданной интенсивности могла передать электрону энергию, достаточную для совершения им работы выхода.
