Задание 1
1. Дайте статистическую характеристику совокупности:
- Произведите аналитическую группировку фирм, разбив их совокупность на 4-5 групп (с равными интервалами) по факторному признаку;
- для более подробной характеристики совокупности по каждой группе и в целом по совокупности определите абсолютные и средние значения величин анализируемых признаков. Оформите в виде статистической таблицы;
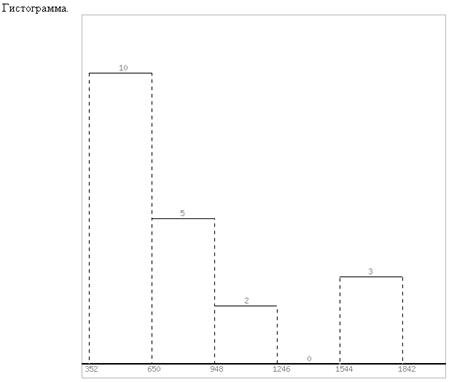
- изобразите графически вариационный ряд распределения (гистограмма распределения);
- рассчитайте основные статистические характеристики:
· средние значения (
, Мо, Me);
· показатели вариации признака (R, 
);
2. На основании группировки сделайте содержательные выводы о структуре совокупности и эффективности деятельности фирм.
3. Сделайте выводы о наличии, направлении и форме связи между двумя взаимосвязанными признаками, один из которых является факторным, другой – результативным. На основании проделанных расчетов сделайте выводы об однородности совокупности и симметричности распределения фирм по изучаемому признаку.
4. По данным аналитической группировки измерьте тесноту связи между изучаемыми признаками, исчислив коэффициент детерминации (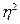
) и эмпирическое корреляционное отношение (η). Сделайте выводы.
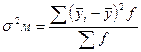- межгрупповая дисперсия;
- среднее значение результата по группе;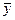 
- общая средняя по совокупности; 
- индивидуальноезначение результативногопризнака у i-й единицы совокупности.
- общая дисперсия;
Таблица 1
Основные финансово-экономические показатели по отрасли за год
| №№ Фирм | Признак 1 | Признак 2 |
| Балансовая прибыль (тыс. руб.) | Коэффициент автономии (доля собственного капитала в активах, %) | |
| А | ||
| 38,1 | ||
| 41,9 | ||
| 46,2 | ||
| 30,9 | ||
| 30,4 | ||
| 37,4 | ||
| 30,6 | ||
| 43,7 | ||
| 42,1 | ||
| 56,5 | ||
| 32,5 | ||
| 30,2 | ||
| 49,2 | ||
| 41,3 | ||
| 52,0 | ||
| 36,7 | ||
| 30,9 | ||
| 37,0 | ||
| 76,1 | ||
| 35,8 |
Решение
Данные группируются по балансовой прибыли. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная.
Тогда ширина интервала составит:
Аналитическая группировка.
| Группы | № | Кол-во, nj | ∑X | Xcp = ∑Xj / nj | ∑Y | Ycp = ∑Yj / nj |
| 352 - 650 | 1,2,3,4,5,6,7,8,9,10 | 467.7 | 351.4 | 35.14 | ||
| 650 - 948 | 11,12,13,14,15 | 755.8 | 206.4 | 41.28 | ||
| 948 - 1246 | 16,17 | 82.9 | 41.45 | |||
| 1246 - 1544 | ||||||
| 1544 - 1842 | 18,19,20 | 1762.33 | 178.8 | 59.6 | ||
| Итого | 789,15 | 819.5 | 40,975 |
Если сделать группировку по 4 группам, то получится группа, которая тоже ничего не содержит.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Аналитическая группировка.
| Группы | № | Кол-во, nj | ∑X | Xcp = ∑Xj / nj | ∑Y | Ycp = ∑Yj / nj |
| 352 - 724.5 | 1,2,3,4,5,6,7,8,9,10,11,12 | 500.83 | 430.9 | 35.91 | ||
| 724.5 - 1097 | 13,14,15,16,17 | 897.2 | 209.8 | 41.96 | ||
| 1097 - 1469.5 | ||||||
| 1469.5 – 1842 | 18,19,20 | 1762.33 | 178.8 | 59.6 | ||
| Итого | 789,15 | 819.5 | 40,975 |
По аналитической группировке измеряют связь при помощи эмпирического корреляционного отношения. Оно основан на правиле разложения дисперсии: общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.
1. Находим средние значения каждой группы.
Общее средние значение для всей совокупности:
2. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением).
Расчет для группы: 352 - 650 (1,2,3,4,5,6,7,8,9,10)
| yj | (yj - yср)2 | Результат |
| 30.6 | (30.6 - 35.14)2 | 20.61 |
| 32.5 | (32.5 - 35.14)2 | 6.97 |
| 38.1 | (38.1 - 35.14)2 | 8.76 |
| 30.2 | (30.2 - 35.14)2 | 24.4 |
| (37 - 35.14)2 | 3.46 | |
| 30.9 | (30.9 - 35.14)2 | 17.98 |
| 30.4 | (30.4 - 35.14)2 | 22.47 |
| 36.7 | (36.7 - 35.14)2 | 2.43 |
| 35.8 | (35.8 - 35.14)2 | 0.44 |
| 49.2 | (49.2 - 35.14)2 | 197.68 |
| Итого | 305.2 |
Определим групповую (частную) дисперсию для 1-ой группы:
Расчет для группы: 650 - 948 (11,12,13,14,15)
| yj | (yj - yср)2 | Результат |
| 37.4 | (37.4 - 41.28)2 | 15.05 |
| 42.1 | (42.1 - 41.28)2 | 0.67 |
| 43.7 | (43.7 - 41.28)2 | 5.86 |
| 41.9 | (41.9 - 41.28)2 | 0.38 |
| 41.3 | (41.3 - 41.28)2 | 0.0004 |
| Итого | 21.97 |
Определим групповую (частную) дисперсию для 2-ой группы:
Расчет для группы: 948 - 1246 (16,17)
| yj | (yj - yср)2 | Результат |
| (52 - 41.45)2 | 111.3 | |
| 30.9 | (30.9 - 41.45)2 | 111.3 |
| Итого | 222.61 |
Определим групповую (частную) дисперсию для 3-ой группы:
Расчет для группы: 1246 - 1544 ()
| yj | (yj - yср)2 | Результат |
| Итого |
Определим групповую (частную) дисперсию для 4-ой группы:
Расчет для группы: 1544 - 1842 (18,19,20)
| yj | (yj - yср)2 | Результат |
| 56.5 | (56.5 - 59.6)2 | 9.61 |
| 76.1 | (76.1 - 59.6)2 | 272.25 |
| 46.2 | (46.2 - 59.6)2 | 179.56 |
| Итого | 461.42 |
Определим групповую (частную) дисперсию для 5-ой группы:
3. Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:
Средняя из частных дисперсий:
4. Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной
δ2 = ((35.14-40.98)2*10 + (41.28-40.98)2*5 + (41.45-40.98)2*2 + (0-40.98)2* + (59.6-40.98)2*3)/20 = 69.1
Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий:
σ2 = 50.56 + 69.1 = 119.66
Проверим этот вывод путем расчета общей дисперсии обычным способом:
| yi | (yi - yср)2 | Результат |
| 30.6 | (30.6 - 40.98)2 | 107.64 |
| 32.5 | (32.5 - 40.98)2 | 71.83 |
| 38.1 | (38.1 - 40.98)2 | 8.27 |
| 30.2 | (30.2 - 40.98)2 | 116.1 |
| (37 - 40.98)2 | 15.8 | |
| 30.9 | (30.9 - 40.98)2 | 101.51 |
| 30.4 | (30.4 - 40.98)2 | 111.83 |
| 36.7 | (36.7 - 40.98)2 | 18.28 |
| 35.8 | (35.8 - 40.98)2 | 26.78 |
| 49.2 | (49.2 - 40.98)2 | 67.65 |
| 37.4 | (37.4 - 40.98)2 | 12.78 |
| 42.1 | (42.1 - 40.98)2 | 1.27 |
| 43.7 | (43.7 - 40.98)2 | 7.43 |
| 41.9 | (41.9 - 40.98)2 | 0.86 |
| 41.3 | (41.3 - 40.98)2 | 0.11 |
| (52 - 40.98)2 | 121.55 | |
| 30.9 | (30.9 - 40.98)2 | 101.51 |
| 56.5 | (56.5 - 40.98)2 | 241.03 |
| 76.1 | (76.1 - 40.98)2 | 1233.77 |
| 46.2 | (46.2 - 40.98)2 | 27.3 |
| Итого | 2393.26 |
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:
Определяем эмпирическое корреляционное отношение:
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая
Коэффициент детерминации.
Определим коэффициент детерминации:
Таким образом, на 57.75% вариация обусловлена различиями между признаками, а на 42.25% – другими факторами.
Средняя взвешенная
Мода
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 352, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 550.67
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 352 - 650, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 650
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 1842 - 352 = 1490
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
Каждое значение ряда отличается от другого не более, чем на 320.35
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Среднее квадратическое отклонение (средняя ошибка выборки).
Каждое значение ряда отличается от среднего значения 813.9 не более, чем на 415.87
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30%,но v<70%, то вариация умеренная.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
Задание 2
Проанализировать интенсивность динамики, средние характеристики и основную тенденцию развития по представленным данным.
Для этого вычислить:
1. Абсолютный прирост, темп роста, темп прироста (цепным и базисным способом), абсолютное значение 1 % прироста;
2. Средний уровень ряда, средний абсолютный прирост, среднегодовой темп роста и прироста;
3. Выравнять ряд с помощью скользящей средней, а также произвести аналитическое выравнивание (функцию выбрать). Изобразить результаты анализа динамики графически.
Таблица 2
Динамика социально-экономических показателей
 Периоды
времени
Показатели
| 1-ый | 2-ой | 3-ий | 4-ый | 5-ый | 6-ой |
| Оборот розничной торговли региона, млн. руб. |
Решение
Абсолютный прирост, темп роста, темп прироста (цепным и базисным способом), абсолютное значение 1 % прироста
Показатели анализа ряда динамики
Показатели анализа ряда динамики могут быть рассчитаны цепным и базисным методами.
Если за базу сравнения принимается неизменная величина (как правило, начальный уровень ряда), то определяют базисные величины.
Если база сравнения меняется, определяют цепные величины.
Показатели анализа ряда:
1) Абсолютный прирост
а) базисный
б) цепной
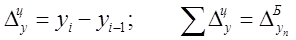
где: 
– базисный абсолютный прирост за конечный уровень.
2) Коэффициент роста
а) базисный
б) цепной
3) Темп роста – это коэффициент роста, выраженный в процентах, т.е.:
а) базисный
б) цепной
4) Коэффициент прироста
а) базисный
,
б) цепной
5) Темп прироста – это коэффициент прироста, выраженный в процентах:
Тприроста = Кприроста * 100
или
Тприроста = Троста – 100
а) базисный
б) цепной
Средние показатели ряда динамики
1) Средний абсолютный прирост – это обобщенная характеристика индивидуальных абсолютных приростов
где: n – число уровней ряда.
2) Средний темп роста
средний коэффициент роста:
3) Средний темп прироста
Для расчетов составим таблицу
| y | Абсолютный прирост | Коэффициент роста | Темп роста | Коэффициент прироста | ||||
| баз | Цеп | баз | Цеп | баз | Цеп | Баз | Цеп | |
| 100,00% | ||||||||
| 1,286 | 1,286 | 128,6% | 128,6% | 0,286 | 0,286 | |||
| 1,506 | 1,171 | 150,6% | 117,1% | 0,506 | 0,171 | |||
| -27 | 1,496 | 0,993 | 149,6% | 99,3% | 0,496 | -0,007 | ||
| 2,138 | 1,429 | 213,8% | 142,9% | 1,138 | 0,429 | |||
| 2,861 | 1,338 | 286,1% | 133,8% | 1,861 | 0,338 |
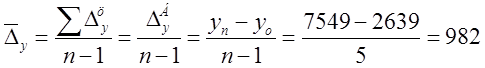
, или 123,4%
Выравнять ряд с помощью скользящей средней, а также произвести аналитическое выравнивание (функцию выбрать). Изобразить результаты анализа динамики графически.
Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| T | y | ys | Формула |
| - | - | ||
| 3336.33 | (2639 + 3395 + 3975)/3 | ||
| 3772.67 | (3395 + 3975 + 3948)/3 | ||
| 4521.33 | (3975 + 3948 + 5641)/3 | ||
| 5712.67 | (3948 + 5641 + 7549)/3 | ||
| 4396.67 |
Линейное уравнение тренда имеет вид y = bt + a
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t•y |
Для наших данных система уравнений имеет вид:
7a0 + 28a1 = 27147
21a0 + 140a1 = 110645
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = 73.46, a1 = 3584.29
Уравнение тренда:
y = 73.46 t + 3584.29
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = 73.46 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на 73.46.
Задание 3
По данным об объеме производства изделий (тыс. шт.) и себестоимости единицы (тыс. руб.) (Таблица 3) исчислить:
индекс себестоимости переменного состава, постоянного состава и структурных сдвигов.
увязать в систему индексов. Дать выводы по каждому из них.
Таблица 3
Сведения об объемах производства и себестоимости продукции
| Изделие | Фирма 1 | Фирма 2 | ||||||
| Себестоимость единицы, д.е. | Производство изделий, шт. | Себестоимость единицы, д.е. | Производство изделий, шт. | |||||
| Базис. период | Отчет. период | Базис. период | Отчет. период | Базис. период | Отчет. период | Базис. период | Отчет. период | |
| ОГР | 3,3 | 3,5 | 2,9 | 2,6 |
Решение
Сведем все в одну таблицу
| Изделие | Фирма 1 | |||
| Себестоимость единицы, д.е. | Производство изделий, шт. | |||
| Базис. период | Отчет. период | Базис. период | Отчет. период | |
| ОГР(фирма1) | 3,3 | 3,5 | ||
| ОГР(фирма 2) | 2,9 | 2,6 |
