Коэффициенты φb для расчета балок на устойчивость

1*. Для балок двутаврового сечения с двумя осями симметрии для определения коэффициента φ_b необходимо вычислить коэффициент φ ₁ по формуле

, (174)

где значения ψ следует принимать по табл. 77 и 78* в зависимости от характера нагрузки и параметра α, который должен вычисляться по формулам:

а) для прокатных двутавров

, (175)

где l_ef - расчетная длина балки или консоли, определяемая согласно требованиям п. 5.15;

h - полная высота сечения;

J_t - момент инерции сечения при кручении;

Таблица 77

Коэффициенты ψ для двутавровых балок с двумя осями симметрии

Количество закреплений сжатого пояса в пролете	Вид нагрузки в пролете	Нагруженный пояс	Формулы для ψ при значениях α
0,1 ≤ α ≤ 40	40 < α ≤ 400
Без закреплений	Сосредоточенная	Верхний	ψ = 1,75 + 0,09α	ψ = 3,3 + 0,053α - 4,5 · 10-5α2
Нижний	ψ = 5,05 + 0,09α	ψ = 6,6 + 0,053α - 4,5 · 10-5α2
Равномерно распределенная	Верхний	ψ = 1,6 + 0,08α	ψ = 3,15 + 0,04α - 2,7 · 10-5α2
Нижний	ψ = 3,8 + 0,08α	ψ = 5,35 + 0,04α - 2,7 · 10-5α2
Два и более, делящих пролет на равные части	Любая	Любой	ψ = 2,25 + 0,07α	ψ = 3,6 + 0,04α - 3,5 · 10-5α2
Одно в середине	Сосредоточенная в середине	Любой	ψ = 1,75 ψ 1	ψ = 1,75 ψ 1
Сосредоточенная в четверти	Верхний	ψ = 1,14 ψ 1	ψ = 1,14 ψ 1
Нижний	ψ = 1,6 ψ 1	ψ = 1,6 ψ 1
Равномерно распределенная	Верхний	ψ = 1,14 ψ 1	ψ = 1,14 ψ 1
Нижний	ψ = 1,3 ψ 1	ψ = 1,3 ψ 1

Примечание. Значение ψ ₁ следует принимать равным ψ при двух и более закреплениях сжатого пояса в пролете.

Таблица 78*

Коэффициенты ψ для жестко заделанных консолей двутаврового сечения с двумя осями симметрии

Вид нагрузки	Нагруженный пояс	Формулы для ψ при отсутствии закреплений сжатого пояса и при значениях α
4 ≤ α ≤ 28	28 < α ≤ 100
Сосредоточенная на конце консоли	Верхний	ψ = 1,0 + 0,16α	ψ = 4,0 + 0,05α
Нижний	ψ = 6,2 + 0,08α	ψ = 7,0 + 0,05α
Равномерно распределенная	Верхний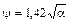

Примечание. При наличии закреплений сжатого пояса в горизонтальной плоскости на конце или по длине консоли коэффициенты ψ следует определять как для консоли без закреплений, кроме случая сосредоточенной нагрузки, приложенной к верхнему поясу на конце консоли, при котором ψ = 1,75 ψ ₁ (значение ψ ₁ следует принимать согласно примеч. табл. 77).

б) для сварных двутавров, составленных из трех листов, а также для двутавровых балок с поясными соединениями на высокопрочных болтах

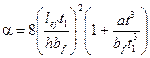, (176)

где обозначено:

для сварных двутавров:

t - толщина стенки;

b_f u t ₁ - ширина и толщина пояса балки;

h - расстояние между осями поясов;

а - размер, равный 0,5 h;

для двутавровых балок с поясными соединениями на высокопрочных болтах:

t - сумма толщин стенки и вертикальных поясных уголков;

b_f - ширина листов пояса;

t ₁ - сумма толщин листов пояса и горизонтальной полки поясного уголка;

h - расстояние между осями пакета поясных листов;

а - ширина вертикальной полки поясного уголка за вычетом толщины горизонтальной полки.

Значение коэффициента φ_b в формуле (34) необходимо принимать:

при φ ₁ ≤ 0,85 φ_b = φ ₁; при φ ₁ > 0,85 φ_b = 0,68 + 0,21 φ ₁, но не более 1,0.

2. Для балок двутаврового сечения с одной осью симметрии (рис. 28) для определения коэффициента φ_b необходимо вычислить коэффициенты φ ₁ и φ ₂ по формулам:

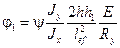; (177)

, (178)

где h ₁ - расстояние от центра тяжести сечения до оси более развитого пояса;

h ₂ - то же, до оси менее развитого пояса;

l_ef - имеет то же значение, что и в формуле (175);

ψ - коэффициент, вычисляемый по формуле

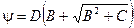; (179)

Коэффициенты D, С и B в формуле (179) следует определять по табл. 79 и 80.

Для двутавровых сечений при 0,9 < n < 1,0 коэффициенты ψ следует определять линейной интерполяцией между значениями, полученными по формуле (179) для двутавровых сечений при п = 0,9 и для тавровых при п = 1.

Для таврового сечения при сосредоточенной или равномерно распределенной нагрузке и α < 40 коэффициенты ψ следует умножать на (0,8 + 0,004α).

При n > 0,7 и 5 ≤ l_ef / b ₂ ≤ 25 значение коэффициента φ ₂ необходимо уменьшить умножением на (1,025 - 0,015 l_ef / b ₂) и принимать при этом не более 0,95.

Значения l_ef / b ₂ > 25 в балках с менее развитым сжатым поясом не допускаются.

Значения коэффициентов φ_b в формуле (34) необходимо принимать по табл. 81, но не более 1,0.

3*. Для балок швеллерного сечения коэффициент φ_b следует определять как для балок симметричного двутаврового сечения; при этом значения α необходимо вычислять по формуле (175), а вычисленные значения φ ₁ умножать на 0,7.

Значения J_x, J_у и J_t в формулах (174) и (175) следует принимать для швеллера.

Рис. 28. Схема двутаврового сечения с одной осью симметрии при изгибе

Таблица 79

Коэффициенты D и С

Вид нагрузки	D	Коэффициент C при сечении
двутавровом п < 0,9	тавровом п = 1
Сосредоточенная в середине пролета	3,265	0,330 μ	0,0826α
Равномерно распределенная	2,247	0,481 μ	0,1202α
Чистый изгиб	4,315	0,101 μ	0,0253α

Обозначения, принятые в табл. 79:

; μ = n (1 - n) (9,87 + α ₁),

где ,

здесь J ₁ и J ₂ - моменты инерции соответственно большего и меньшего поясов относительно оси симметрии сечения;

α - следует определять по формуле (175), в которой момент инерции сечения при кручении ,

где b_i и t_i - соответственно ширина и толщина листов, образующих сечение; δ = 1,25 - для двутаврового сечения с одной осью симметрии; δ = 1,20 - для таврового сечения.

Таблица 80

Коэффициент В

Схема сечения и место приложения нагрузки	Коэффициент В при нагрузке
сосредоточенной в середине пролета	равномерно распределенной	вызывающей чистый изгиб
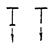
	δ	μ	β
	δ -1	μ -1	β
	1- δ	1- μ	- β
	- δ	- μ	- β

Обозначения, принятые в табл. 80:

δ = п + 0,734 β; μ = n + 1,145 β;

,

где b ₁ - ширина более развитого пояса балки;

n - обозначение то же, что и в табл. 79.

Таблица 81

Коэффициенты φ_b

Значение φ 2	Коэффициенты φb при сжатом поясе
более развитом	менее развитом
φ 2 ≤ 0,85	φb = φ 1	φb = φ 2
φ 2 > 0,85		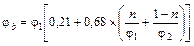φb = 0,68 + 0,21 φ 2

Таблица 82

Моменты инерции при кручении J_t прокатных двутавров по ГОСТ 8239-72*

Номер двутавра	Jt, см4
	2,28
	2,88
	3,59
	4,46
	5,60
18а	6,54
	6,92
20а	7,94
	8,60
22а	9,77
	11,1
24а	12,8
	13,6
27а	16,7
	17,4
30а	20,3
	23,8
	31,4
	40,6
	54,7
	75,4

ПРИЛОЖЕНИЕ 8