Сущность метода заключается в нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических полученных по выбранному уравнению регрессии.


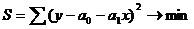
 для линейной зависимости
для линейной зависимости
где n – объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных факторов; параметр а1 – коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
Линейный коэффициент корреляции. Значимость данного коэффициента. Индекс детерминации
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Виды зависимостей:
1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком)
2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков
3) множественная корреляция – зависимость результативного и двух и более факторных признаков.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками.
Теснота связи количественно выражается величиной коэффициентов корреляции.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

Линейный коэффициент корреляции изменяется в пределах от -1 до+1. Чем ближе он по модулю к единице, тем теснее связь. Знак указывает направление связи. Знак "+" прямая связь, знак "-" обратная связь.
По степени тесноты связи различают количественные критерии оценки тесноты связи:
| Величина коэффициента корреляции | Характер связи |
| До ±0,3 | Практически отсутствует |
| ±0,3 – ±0,5 | Слабая |
| ±0,5 – ±0,7 | Умеренная |
| ±0,7 – ±1,0 | Сильная |
Коэффициент детерминации
Изменение результативного признака y обусловлено вариацией факторного признака x. Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует коэффициент детерминации R2. Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции:
R2 = rxy2
где rxy - коэффициент корреляции.
В общем случае, коэффициент детерминации находится по формуле:







