ГРУППА АТП-21
ПРЕПОДАВАТЕЛЬ: Резникова С.А.
Задания на курсовую работу
- Студенту предлагается выполнить курсовую работу на тему: «Расчет кинематических характеристик движущихся механизмов». В задачах данной работы определяются координаты, скорость, ускорение точки в любой назначенный момент времени при различных способах задания движения.
- Создать программу на языке Delphi. Результаты оформить в виде таблицы и графиков.
- Промоделировать движение системы путем графической анимации.
- Создать проект в среде MathCAD. Результаты оформить в виде таблицы и графиков.
- Сравнить результаты, полученные в пунктах 2 и 4.
Пояснения к поставленной задаче
Из всех способов задания движения точки наибольшее распространение получили координатный и естественный способы.
Рассмотрим вначале координатный способ задания движения точки. Положение в пространстве движущейся точки определяется тремя координатами в декартовой системе координат. Эти координаты задаются как функции времени:
; 
; 
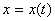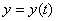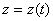. (1)
Зависимости (1) называются уравнениями движения точки в декартовых координатах.
Если движение точки происходит в плоскости ху, то задаются только два уравнения движения:
; .
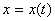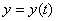При прямолинейном движении точки достаточно задать одно уравнение движения:
.
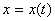если принять, что ось х совпадает с прямой, по которой движется точка.
Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени.
При задании движения точки уравнениями (1) проекции скорости на оси декартовых координат равны:
; 
; 
.
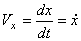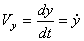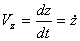Модуль скорости
. (2)
Направление скорости определяется направляющими косинусами:
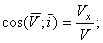
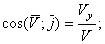
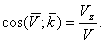
Если движение точки задается в плоскости ху, то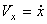 
; 
;
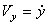
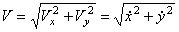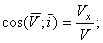
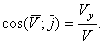
При прямолинейном движении по оси х:
; 
.
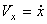Характеристикой быстроты изменения скорости является ускорение а. Ускорение точки равно производной от вектора скорости по времени:
.
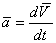При задании движения точки уравнениями (1) проекции ускорения на координатные оси равны:
; 
; 
.
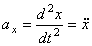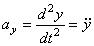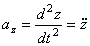Модуль ускорения:
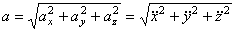. (3)
Направление ускорения определяется направляющими косинусами
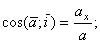
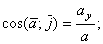
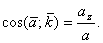
Если движение точки задается в плоскости ху, то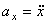 
; 
;
;
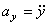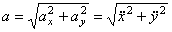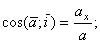
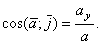
При прямолинейном движении по оси х
; 
.
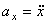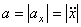Далее рассмотрим естественный способ задания движения точки.
Считается, что движение точки задано естественным способом, если указаны ее траектория и закон изменения криволинейной координаты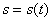 
. Уравнение 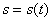называется законом движения точки по траектории. При этом на траектории указывается начало отсчета, а также положительное направление отсчета координаты s в виде стрелки 
.
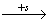Модуль скорости точки определяется по формуле
. (4)
Вектор скорости V направлен по касательной к траектории в сторону стрелки 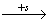, если 
, и в противоположную сторону, если 
.
Ускорение точки определяется как векторная сумма касательного и нормального ускорений точки:
.
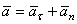Модуль касательного ускорения определяется по формуле
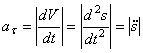. (5)
Вектор касательного ускорения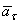 
направлен по касательной к траектории в сторону стрелки 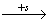, если 
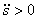, и в противоположную, если 
.
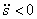Модуль нормального ускорения определяется по формуле
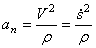, (6)
где 
– радиус кривизны траектории в данной точке.
Вектор нормального ускорения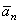 
всегда направлен по главной нормали в сторону центра кривизны траектории.
Модуль полного ускорения
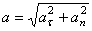. (7)
Если движение точки задано координатным способом, то можно определить параметры движения, характерные для естественного способа задания движения.
Так можно, например, по уравнениям движения точки (1) найти уравнение ее траектории в форме зависимости между координатами. Для этого надо из уравнений движения исключить время t. Затем можно найти закон движения точки по траектории 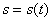, используя формулу (4). Из этой формулы следует, что 
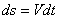; с учетом формулы (2) имеем 
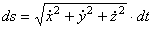и 
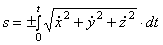. (8)
В законе движения (8) за начало отсчета координаты s принимается начальное положение точки, когда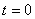 
. Знак “плюс” или “минус” перед интегралом ставится в зависимости от выбора положительного направления отсчета координаты s: если движение точки начинается в сторону стрелки 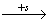, то следует брать знак “плюс”, в противном случае – знак “минус”.
Рассмотрим случай, когда движение точки задается в полярных координатах. Пусть точка М движется все время в одной и той же плоскости. Тогда ее положение можно определить полярными координатам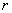и 
и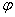 
(рис.1)
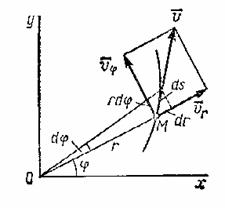
Рис.1
При движении точки 
эти координаты с течением времени изменяются. Следовательно, закон движения точки в полярных координатах будет задаваться уравнениями
, 
.
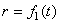Скорость точки численно равна отношению элементарного перемещения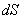 
к промежутку времени 
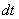, то есть 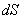/ 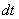. В данном случае перемещение 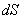геометрически слагается из радиального перемещения, численно равного 
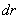, и поперечного перемещения, перпендикулярного радиусу 
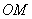и численно равного 
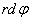. Следовательно, сама скорость 
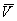будет геометрически складываться из радиальной скорости 
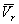и поперечной (трансверсальной) скорости 
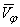, численно равных
, 
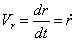. (9)
Так как 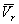и 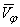взаимно перпендикулярны, то модуль скорости точки 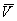определится по формуле
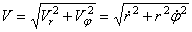. (10)
Формулы (9) и (10) определяют скорость точки в полярных координатах при плоском движении.
Ниже приводятся (без вывода) формулы для определения проекций ускорения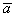 
на радиальное и трансверсальное направления, а также для определения его модуля
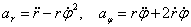, (11)
.
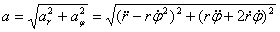Рассмотрим примеры решения задач.
Алгоритм решения задачи
1. Для получения уравнения траектория вида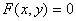 
исключить из уравнений движения время t:
2. Построить уравнение траектории
3. Для определения положения точки в начальный момент времени необходимо подставить значение 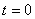в уравнения движения
4. Определить точки пересечения с осью х и с осью y.
5. Для определения закона движения точки по траектории воспользоваться формулой:
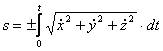, при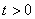 
,
6. Определить направление (положительное либо отрицательное), найти S.
7. Чтобы найти уравнение траектории точки необходимо из уравнений движения исключить время. Для этого уравнения движения разрешить относительно функций и возвести полученные результаты в квадрат. Сложить эти уравнения.
Для определения положения точки в начальный момент времени необходимо подставить значение 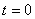в уравнения движения.
Определить точки пересечения с осью х и с осью y.
Для определения закона движения точки по траектории воспользуемся формуло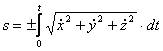й , при 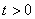, найти S.
Определить время Т прохождения точкой полной окружности, Т – время, по истечении которого s станет равным длине окружности:
2pR=(3p/2)*T
8. Чтобы найти уравнение траектории точки вывести из уравнения 
время t и возвести полученные результаты в квадрат.
Уравнение траектории получается суммированием полученных уравнений.
Модуль скорости точки определяется по формуле 
.
При t=0: Vx=… и Vy=…., тогда V=….
При t=1c: Vx=… и Vy=…, тогда V=…..
Модуль ускорения точки определяется по формуле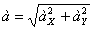 
При t=0: ax=… ay=…,тогда a0=….,
При t=1c: ax=… ay=…,тогда a0=….
