2.1. Изучить возможности языка программирования для реализации вычислительного процесса вложенной циклической структуры с известным числом повторений в цикле.
2.2. Разработать алгоритм решения в соответствии с заданием.
2.3. Составить программу табулирования функции.
2.4. Подготовить тесты для проверки правильности функционирования программы.
Задания к работе
Выполнить программу на ЭВМ с использование вложенных циклов. В программе указать название работы, фамилию исполнителя, группу и номер варианта задания. На печать вывести значения вводимых исходных данных и результаты вычислений.
Варианты заданий
1. Дано натуральное число n и действительные числа 
. Получить
.
2. Дано натуральное число n. Получить f 0× f 1×...× f n, где
.
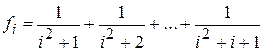3. Даны натуральные числа n, m и действительные числа а 1... а n. Получить последовательность b 1... b n, где
, 
,..., 
.
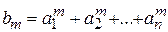4. Дано натуральное число n. Найти натуральное число от 1 до n с максимальной суммой делителей.
5. Дано натуральное число n. Получить все простые делители этого числа.
6. Даны натуральные числа a, b (a £ b). Получить все простые числа p, удовлетворяющие неравенствам a £ p £ b.
7. Дано натуральное число n. Найти n первых простых чисел.
8. Даны натуральные числа n и m. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m.
9. Дано натуральное число n. Получить все совершенные числа, меньше n.
10. Даны натуральные числа n и m. Вычислить
.
11. Даны натуральные числа n и m. Вычислить
.
12. Дано натуральное число n. Вычислить
.
13. Дано натуральное число n. Вычислить
.
14. Дано натуральное число n и действительное число х. Вычислить
.
15. Дано натуральное число n и действительное число х. Вычислить
.
16. Дано натуральное число n и действительное число х. Вычислить
.
17. Дано натуральное число n и целые числа а 1... а n. Получить все числа, которые входят в последовательность по одному разу.
18. Дано натуральное число n и целые числа а 1... а n, b 1... b n. Получить все члены последовательности а 1... а n, которые не входят в b 1... b n.
19. Дано натуральное число n и целые числа а 1... а n. Получить все числа, которые входят в последовательность более чем по одному разу.
20. Дано натуральное число n и целые числа а 1... а n. Для каждого из чисел а 1... а n определить, сколько раз оно входит в данную последовательность.
21. Дано натуральное число n, целые числа m, а 1... а n. Найти три натуральных числа i, j, k, каждое из которых не превосходит n, такие, что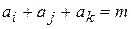 
. Если таких чисел нет, то сообщить об этом.
22. Дано натуральное число n и целые числа а 1... а n. Найти в последовательности а 1... а n числа, модуль разности которых имеет наибольшее и наименьшее значение.
23. Дано натуральное число n. Можно ли представить его в виде суммы трех квадратов натуральных чисел? Если можно, то указать все тройки x, y, z таких натуральных чисел, что n = x 2+ y 2+ z 2.
24. Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел (теорема Лагранжа). Дано натуральное число n. Указать такие неотрицательные целые a, b, c, d, что n = a 2+ b 2+ c 2 +d 2.
25. Дано натуральное число n и действительные числа х, у 1... у n. В последовательности у 1... у n найти два члена, среднее арифметическое которых ближе всего к х.
26. Даны натуральные числа n и m. Вычислить число сочетаний
.
27. Дано натуральное число n. Вычислить
.
28. Дано натуральное число n и действительное число х. Вычислить
.
29. Дано натуральное число n. Вычислить
.
30. Дано натуральное число n. Вычислить
.
Примечания
1. Натуральное число называется простым, если оно делится без остатка лишь на 1 и само на себя.
2. Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением себя самого. Число 6 - совершенное, так как 6 = 1+2+3. Число 8 - не совершенное, так как 8 ¹ 1+2+4.
3. Число называется полным квадратом, если оно может быть представлено в виде суммы квадратов двух натуральных чисел.
ЛАБОРАТОРНАЯ РАБОТА №3
