ПОСТРОЕНИЕ УРАВНЕНИЙ РЕГРЕССИИ.
МОДУЛЬ MULTIPLE REGRESSION СИСТЕМЫ STATISTICA.
Цель занятия:
1. Изучить структуру и назначение статистического модуля Multiple Regression системы STATISTICA.
2. Освоить основные приемы работы в модуле Multiple Regression системы STATISTICA.
3. Освоить процедуру построения линейной регрессии в модуле Multiple Regression.
4. Самостоятельно решить задачу о нахождении коэффициентов линейной регрессионной модели.
Общие положения.
Статистический модуль Multiple Regression – Множественная регрессия включает в себя набор средств проведения регрессионного анализа данных.
Линейный регрессионный анализ.
В линейный регрессионный анализ входит широкий круг задач, связанных с построением зависимостей между группами числовых переменных X º (x 1 ,..., xp) и Y = (y 1 ,..., ym).
Предполагается, что Х - независимые переменные (факторы) влияют на значения Y - зависимых переменных (откликов). По имеющимся эмпирическим данным (Xi, Yi), i = 1,..., n требуется построить функцию f (X), которая приближенно описывала бы изменение Y при изменении X. Искомая функция записывается в следующем виде: f (X) = f (X, q) + e, где q - неизвестный многомерный параметр, e - случайная составляющая с нулевым средним, f (X, q) является условным математическим ожиданием Y при условии известного X и называется регрессией Y по X.
Простая линейная регрессия.
Функция f (x, q) имеет вид f (x, q) = A + bx, где q = (A, b) - неизвестные параметры. Относительно имеющихся наблюдений (xi, yi), где i = 1,..., n, полагаем, что yi = A + bxi + ei. e1 ,..., e n – ошибка вычисления Y по принятой модели. Для нахождения параметров широко используют метод наименьших квадратов.
Значения параметров модели находят из уравнения:
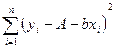
= min по (A, b)
Чтобы упростить формулы, положим xi = xi -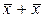 
; получим:
yi = a + b (xi -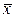 
) + ei, i = 1,..., n,
где =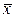 
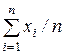, a = A + b 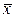. Сумму 
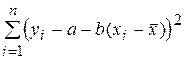минимизируем по (a,b), приравнивая нулю производные по a и b; получим систему линейных уравнений относительно a и b. Ее решение (
) легко находится:
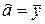, где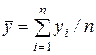 
,
.
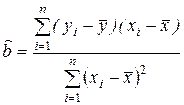Свойства оценок. Нетрудно показать, что если M e i = 0, D e i = s2, то
1) M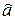 
= а, М 
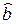= b, т.е. оценки несмещенные;
2) D 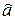= s2 / n, D 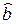= s2 / 
;
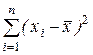3) cov (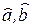
) = 0;
если дополнительно предположить нормальность распределения e i, то
4) оценк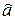и и 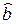нормально распределены и независимы;
5) остаточная сумма квадратов
Q 2 =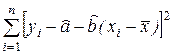 
независима от (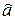, 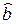), а Q 2 / s2 распределена по закону хи-квадрат 
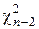с n -2 степенями свободы.
Вызов статистического модуля Multiple Regression – Множественная регрессия выполним используя пиктограмму в левом нижнем углу (рис.1). В стартовом диалоговом окне этого модуля (рис. 2) при помощи кнопки Variables указываются зависимая (dependent) и независимые(ая) (independent) переменные.
В поле MD deletion указывается способ исключения из обработки недостающих данных:
casewise - игнорируется вся строка, в которой есть хотя бы одно пропущенное значение;
mean Substitution - взамен пропущенных данных подставляются средние значения переменных;
pairwise - попарное исключение данных с пропусками из тех переменных, корреляция которых вычисляется.
При необходимости выборочного включения данных для анализа следует воспользоваться кнопкой select cases.
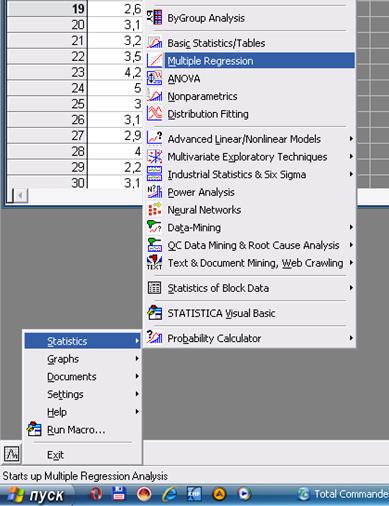
Рисунок – 1 Вызов статмодуля Multiple Regression
Рисунок – 2 Диалоговое окно Multiple Regression
После выбора всех параметров анализа нажмите кнопку OK.
Стандартная линейная модель имеет вид:
Y = a1 + a2X1 + + a3X2 + + a3X3 + ……+ + anXn
Нажатие на кнопку ОК приведет к появлению окна Multiple Regressions Results (результаты регрессионного анализа) (рис. 3), с помощью которого можно просмотреть результаты анализа в деталях.
Рисунок – 3 Окно Multiple Regressions Results (результаты регрессионного анализа)
Окно результатов имеет следующую структуру. Верхняя часть окна – информационная. Нижняя часть окна – содержит функциональные кнопки, позволяющие получить дополнительную информацию об анализе данных.
В верхней части окна приводятся наиболее важные параметры полученной регрессионной модели:
Dependent – имя зависимой переменной (Y);
Multiple R - коэффициент множественной корреляции;
Характеризует тесноту линейной связи между зависимой и всеми независимыми переменными. Может принимать значения от 0 до 1.
R2 или RI - коэффициент детерминации;
Численно выражает долю вариации зависимой переменной, объясненную с помощью регрессионного уравнения. Чем больше R2, тем большую долю вариации объясняют переменные, включенные в модель.
No. Of Cases – число случаев, по которым построена регрессия;
adjusted R - скорректированный коэффициент множественной корреляции;
Этот коэффициент лишен недостатков коэффициента множественной корреляции. Включение новой переменной в регрессионное уравнение увеличивает RI не всегда, а только в том случае, когда частный F-критерий при проверке гипотезы о значимости включаемой переменной больше или равен 1. В противном случае включение новой переменной уменьшает значение RI и adjusted R2.
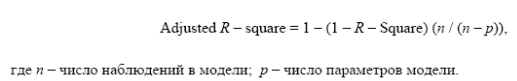
adjusted R2 или adjusted RI - скорректированный коэффициент детерминации;
Скорректированный R2 можно с большим успехом (по сравнению с R2) применять для выбора наилучшего подмножества независимых переменных в регрессионном уравнении
F - F-критерий;
df - число степеней свободы для F-критерия;
p - вероятность нулевой гипотезы для F-критерия;
Standard error of estimate - стандартная ошибка оценки (уравнения);
Intercept - свободный член уравнения, параметр а1;
Std.Error - стандартная ошибка свободного члена уравнения;
t - t-критерий для свободного члена уравнения;
p - вероятность нулевой гипотезы для свободного члена уравнения.
Beta - b-коэффициенты уравнения.
Это стандартизированные регрессионные коэффициенты, рассчитанные по стандартизированным значениям переменных. По их величине можно сравнить и оценить значимость зависимых переменных, так как b-коэффициент показывает на сколько единиц стандартного отклонения изменится зависимая переменная при изменении на одно стандартное отклонение независимой переменной при условии постоянства остальных независимых переменных. Свободный член в таком уравнении равен 0.
При помощи кнопок диалогового окна Multiple Regressions Results (рис. 3) результаты регрессионного анализа можно просмотреть более детально.
Кнопка Summary: Regression results - позволяет просмотреть основные результаты регрессионного анализа (рис. 4, 5): BETA - b-коэффициенты уравнения; St. Err. of BETA - стандартные ошибки b-коэффициентов; В - коэффициенты уравнения регрессии; St. Err. of B - стандартные ошибки коэффициентов уравнения регрессии; t (95) - t-критерии для коэффициентов уравнения регрессии; р-level - вероятность нулевой гипотезы для коэффициентов уравнения регрессии.
Рисунок - 4
Таким образом в результате проведенного регрессионного анализа получено следующее уравнение взаимосвязи между откликом (Y) и независимой переменной (Х):
Y = 17,52232 – 0,06859Х
Свободный коэффициент уравнения значим на 5% уровне (p-level < 0,05). Коэффициентом при Х следует пренебречь. Это уравнение объясняет только 0,028% (R2 = 0,000283) вариации зависимой переменной.
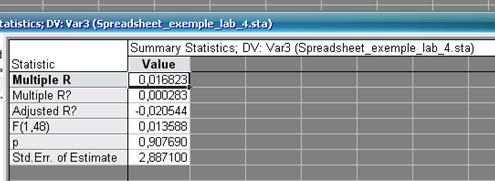
Рисунок - 5
Рассмотрите пример оптовых цен за одну бутылку марочного вина (зависимая переменная) от года закладки вина (независимая переменная).
Множественная регрессия.
