Краткие теоретические сведения
Дифракцией называетсясовокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью (при прохождении через отверстия в экранах, вблизи границ непрозрачных тел и т.п.).
В более узком смысле под дифракцией понимают огибание светом встречных препятствий и проникновении его в область геометрической тени, т.е. отклонение от законов геометрической оптики. Самым наглядным проявлением явления дифракции является нарушение светом закона прямолинейного распространения, возникающее после прохождения светом через малое отверстие в преграде. Условием наблюдения дифракции света является определенное соотношение между диаметром отверстия D и расстоянием b от отверстия до точки наблюдения, а именно: b ~ 103. D.
Принцип Гюйгенса-Френеля: каждая точка, до которой доходит фронт световой волны, становится источником вторичных когерентных световых волн, интерферирующих между собой. Поверхность, огибающая эти вторичные волны (с учетом их интерференции), дает положение волнового фронта световой волны в каждый момент времени. Интенсивность света в каждой точке пространства по ходу светового пучка можно рассматривать как результат интерференции вторичных световых волн.
Метод зон Френеля.
Применим принцип Гюйгенса-Френеля для нахождения амплитуды светового колебания, возбуждаемого в точке Р сферической волной, распространяющейся в однородной среде из точечного источника S. (рис.1.) Для этого необходимо сложить все световые волны, которые приходят в точку наблюдения Р со всех точек волнового фронта S. Френель предложил разделить волновую поверхность на кольцевые зоны таким образом, чтобы края соседних зон отстояли от точки наблюдения Р на расстояния, различающиеся на половину длины световой волны в данной среде, то есть на l /2. (λ — длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны носят название зон Френеля.
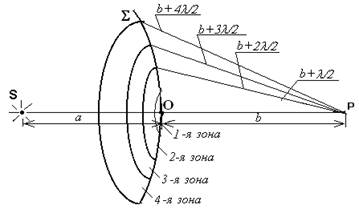
Рис. 1 Метод зон Френеля
В этом случае расстояние от зоны с номером m до точки наблюдения Р будет:
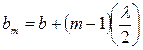(1)
где m = 1, 2, 3... - номер зоны Френеля.
Колебания, приходящие в точку наблюдения Р от краев двух соседних зон, будут находиться в противофазе. Это также относится к любой паре точек, находящихся на поверхностях соседних зон, для которых расстояния до точки наблюдения Р различаются на l/2.
Без вывода запишем, что площади зон Френеля рассчитываются по формуле (2), где а расстояние от точечного источника света S до волнового фронта S, а расстояние Ь – от волнового фронта до точки Р.
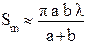(2)
В эту формулу не входит номер зоны. Это означает: при не слишком больших значениях номеров зон m площади всех зон Френеля примерно одинаковы.
Следовательно, каждая зона Френеля содержит одинаковое число светящихся точек (вторичных источников когерентных волн). Вследствие этого для каждой точки в любой зоне Френеля и в соседней с ней зоной Френеля найдется одна и только одна точка, такая, что световые колебания от этой пары вторичных источников приходят в точку наблюдения дифракционной картины с разностью хода l/2. Следовательно, световые колебания от любых двух соседних зон в точке наблюдения Р взаимно гасят друг друга.
Для радиуса внешней границы m-й зоны Френеля получим выражение
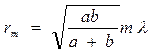(3)
Дифракция на малом отверстии.
Поставим между точечным источником S и точкой наблюдения Р непрозрачный экран с круглым отверстием АВ, плоскость которого перпендикулярна к оси SР. Согласно Френелю, действие такого препятствия cводится к тому, что экран как бы устраняет ту часть волнового фронта, которую он прикрывает.
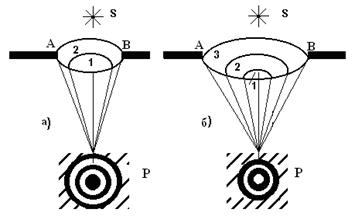Рис.2. Дифракционная картина в случаях:
а) двух зон Френеля;
б) трех зон Френеля.
|
Так, в случае открытых двух зон Френеля увидим в центре экрана темное пятно, а вокруг него светлый поясок (светлое кольцо). Если же увеличить диаметр отверстия, так, что будут открыты три зоны Френеля, то вид картины изменится. Две зоны взаимно гасят друг друга, а третья зона Френеля даст освещение в точке Р. На экране будет видно центральное яркое пятно, а вокруг него чередующиеся темные и светлые кольца (рис.2).
Полученную закономерность мы можем распространить на любое количество зон Френеля, укладывающихся в волновом фронте, выходящем из отверстия.
Вывод: При наблюдении дифракции света на малом отверстии в условиях, когда относительно точки наблюдения во фронте световой волны укладывается четное число зон Френеля, в центре дифракционной картины будет темное пятно, окруженное чередующимися светлыми и темными кольцами. Если же в данных условиях в волновом фронте укладывается нечетное число зон Френеля, то в центре картины будет светлое пятно, окруженное системой темных и светлых колец. Размеры колец тем меньше, чем больше диаметр отверстия, и зависят от длины световой волны.
Дифракция от щели
Немецкий физик Джозеф. Фраунгофер (1787-1826) рассмотрел дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.
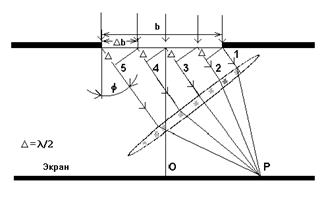
Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис.3).Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении φ,
∆ = NF = α sin φ, (4)
Дифракционная картина, получаемая в параллельных лучах после прохождения светом щели, зависит от числа зон Френеля, укладывающихся в плоскости этой щели.
Рис.3.Наблюдение дифракции Фраунгофера от щели
|
F — основание перпендикуляра, опущенного из точки М на луч ND.
Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т. е. всего на ширине щели уместится m зон Френеля (m=D:λ/2). Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.
Из выражения (4) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла φ. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то
a sin φ = ± 2m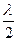 
(m = 1, 2, 3,…),(5)
и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечётно, то
a sin φ = ± (2m + 1) 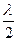(m = 1, 2, 3,…)(6)
и наблюдается дифракционный максимум, соответствующий действию одной не скомпенсированной зоной Френеля. Отметим, что в направлении φ = 0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В0 наблюдается центральный дифракционный максимум.
Изменяя ширину щели, мы меняем число возможных зон Френеля m, открывающихся при наблюдении под данным углом j. Из опыта и соответствующих расчетов следует:
1. если ширина щели равна половине длины волны, то возникает только один нулевой максимум, при j = 900;
2. дальнейшее сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это, естественно, относится и к другим максимумам);
3. при увеличении ширины щели (a > λ) дифракционная картина становится ярче, но дифракционные полосы уже, а число самих полос больше;
4. при ширине щели a» λ в центре получается резкое изображение источника света, т. е. имеет место прямолинейное распространение света;
5. положение дифракционных максимумов зависит от длины волны λ, поэтому рассмотренная выше дифракционная картина имеет место лишь для монохроматического света.
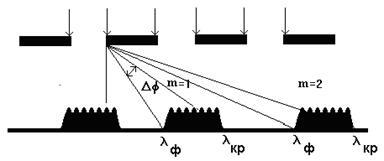
При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при φ=0 разность хода равна нулю для всех λ). Боковые максимумы радужно окрашены, так как условие максимума при любых m различно для разных λ. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m = 1), второго (m = 2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.
Более резкое разрешение максимумов и минимумов освещенности удается получить при дифракции на нескольких щелях, причем, чем больше количество щелей N, тем отчетливее различимы максимумы и минимумы получающейся дифракционной картины.
Дифракционная решетка.
Дифракционная решетка получается при помощи нанесения на прозрачную пластинку системы параллельных равноотстоящих рисок, которые представляют собой преграды свету. Риски можно нанести также на зеркальную металлическую поверхность, в этом случае дифракционная решетка называется отражательной.
|
Сумма ширины прозрачного и непрозрачного штрихов называется периодом дифракционной решетки и обозначается d (d=a+b).
У лучших современных решеток период может быть менее 0,8 мкм, а число штрихов на миллиметр достигает, таким образом, 1200.
Направим на дифракционную решетку параллельный пучок монохроматического света (т.е. света с определенной длиной волны l).
На экране, расположенном по другую сторону дифракционной решетки, будем наблюдать дифракционную картину, состоящую из чередующихся светлых и темных полос. Для того, чтобы в точке наблюдения Р был максимум освещенности, необходимо, чтобы выполнялось условие:
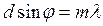(7)
где m = 1,2,3... - целое число.
Приведенное выражение называется формулой дифракционной решетки. Таким образом, перемещая точку наблюдения вдоль линии ОP, мы будем видеть чередующиеся максимумы и минимумы освещенности, соответствующие приведенному выше условию, которые называются главными максимумами. Т.к. в точку наблюдения Р приходят лучи от всех щелей решетки и, складываясь, усиливаются, то максимумы на дифракционной картине выражены тем более четко, чем больше штрихов в дифракционной решетке N.
Между главными максимумами на экране располагается N-2 вторичных максимумов. Однако их интенсивность мала, не более 5% от интенсивности главных максимумов. Центральный главный максимум на экране называется нулевым, от него вправо и влево идут главные максимумы 1, 2, 3... и т.д. порядков. Из геометрических построений можно определить углы, под которыми будут наблюдаться главные максимумы. Угловое положение максимумов и минимумов интенсивности:
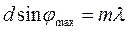
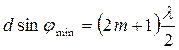(8)
Из формулы дифракционной решетки видно, что угловое положение максимумов и минимумов зависит от длины волны света. Это означает: при наблюдении дифракции сложного света (т.е. содержащего в своем составе излучение нескольких длин волн), напр., белого, дифракционные максимумы для различных компонент этого света будут располагаться на некотором расстоянии друг от друга, т.е. решетка разлагает сложный свет на монохроматические составляющие.
При наблюдении картины дифракции белого цвета каждый дифракционный максимум будет окрашен во все цвета, входящие в состав белого света. Фиолетовый край каждого дифракционного максимума будет обращен к нулевому максимуму. Таким образом, дифракционная решетка представляет собой спектральный прибор. Его чувствительность к определению минимального интервала длин волн света характеризуется величиной угловой дисперсии D:
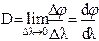(9)
Чем больше величина угловой дисперсии решетки, тем с большей точностью решетка может выделить определенную длину волны света, или, другими словами, тем больший угловой размер занимает интерференционный максимум для белого света, содержащего все длины волн видимого излучения.
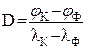(10)
Угловая дисперсия дифракционной решетки прямо пропорциональна числу щелей на единицу длины решетки и обратно пропорциональна косинусу угла наблюдения, т.е. дисперсия возрастает с увеличением порядка наблюдаемого максимума.
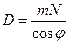(11)
здесь N - число щелей решетки на единицу длины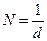 
, m - номер максимума.
|
Рис. 5 Угловая дисперсия дифракционной решетки
Зная период дифракционной решетки, ее можно использовать для определения длины световой волны.
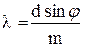(12)
Лабораторная установка
На специальном держателе укреплена дифракционная решетка (Д) и черный экран (Э)с узкой вертикальной щелью по середине. Экран может перемещаться вдоль держателя, что позволяет изменять расстояние между ним и дифракционной решеткой. На экране и держателе имеются миллиметровые шкалы. За экраном закреплен осветитель (О).
Дифракционная решетка устанавливается на расстоянии R=37 см от экрана со щелью. Если смотреть сквозь решетку и щель на осветитель (лампу накаливания), то на черном фоне экрана наблюдаются по обе стороны от щели дифракционные спектры 1-го, 2-го и т.д. порядков. Схема установки показана на рис.6.
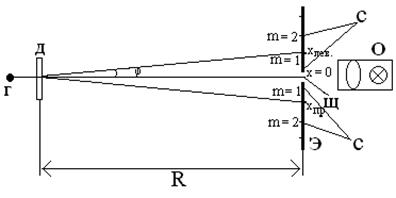Д – дифракционная решетка; Э – экран; О – осветитель; С – дифракционные спектры; Щ – центральная щель; Г – глаз наблюдателя, начало отсчета Х=0.
Рис. 6
|
Угол φ под которым наблюдаются дифракционные максимумы, соответствующие длине волны λ, мал, поэтому можно определить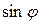 
по формуле
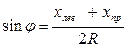(13)
Подставляя значение sinφ из выражения (13) в формулу (7), дающую условие главных максимумов, получим выражение
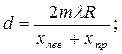(14)
Порядок выполнения работы
Задание 1.Определение периода дифракционной решетки.
1. Измерьте расстояние от нулевого максимума до красной линии справа (хпр) для дифракционных спектров первого (m=1) и второго (m=2) порядков по линейке экрана. Измерения повторите по три раза.
2. Измерьте расстояние от нулевого максимума до красной линии слева (хлев) для дифракционных спектров первого (m=1) и второго (m=2) порядков. Измерения повторите по три раза.
3. Считая длину волны для красного цвета известной и равной λ=6800А0=6,8·10-4 мм вычислите по формуле (14) период дифракционной решетки.
4. Измерения и вычисления занесите в таблицу 1:
Таблица 1
| Порядок спектра m | хпр (мм) | хлев (мм) | d (мм) | d ср (мм) |
Задание 2. Определение длины световой волны.
Зная постоянную дифракционной решетки из первого задания определите неизвестную длину волны по формуле (15):
(15)
Аналогично пунктам 1 и 2 первого задания измерьте расстояние от нулевого максимума до жёлтой, зелёной и фиолетовой линий. Измерения повторите по три раза.
2. Определите длину волны для этих цветов по формуле (15). Результаты измерений и вычислений занесите в таблицу 2:
Таблица 2
| Порядок спектра m | жёлтый | зелёный | фиолетовый | |||||||
| хпр | хлев | λж | хпр | хлев | λз | хпр | хлев | Λф | ||
| Ср.знач. | λж= | λз= | λф= | |||||||
Содержание отчета
В отчете должны быть представлены следующие разделы:
1. Цель работы.
2. Необходимые для расчетов формулы.
3. Таблица результатов.
4. Выводы.
Контрольные вопросы
1. Сформулируйте принцип Гюйгенса-Френеля.
2. В чём заключается явление дифракции и каковы условия наблюдения?
3. В чём отличие дифракционной картины, даваемой одной щелью от картины, получаемой с помощью дифракционной решетки?
4. Что называется периодом дифракционной решетки?
5. Каков порядок следования цветов в дифракционных спектрах?
6. В чём отличие спектра, даваемого дифракционной решеткой от призматического спектра?
7. От чего зависит разрешающая способность решетки?
8. Почему интенсивность линий уменьшается от увеличения порядка спектра?
УИРС
1. Определить изменение дифракционной картины, если закрыть половину решетки. Провести наблюдение и сделать вывод.
2. Определить изменение дифракционной картины, если на решетку направить лучи под большим углом падения. Провести наблюдение и сделать вывод.
3. Рассчитайте угловую дисперсию дифрешетки по формуле (6).
