4.1.1. Включите питание осциллографа, дайте прибору прогреться в течение 15 минут.
4.1.2. В режиме временной развертки луча (переключатель «ВРЕМЯ/ДЕЛ» в положении 1мсек/дел) с помощью соответствующих ручек управления получите временную развертку луча по каналу 1 (на экране осциллографа должна наблюдаться горизонтальная линия, совмещенная с осью Х). Вращением ручек «ЯРКОСТЬ» и «ФОКУС» получите оптимальную для наблюдения яркость и минимальную толщину линии развертки.
4.1.3. Подайте на вход канала Х сигнал с генератора. С помощью переключателей «В/ДЕЛ» и «ВРЕМЯ/ДЕЛ» получите осциллограмму сигнала. Размер осциллограммы должен быть оптимальным для наблюдения. При проведении точных измерений необходимо ручки плавного изменения коэффициента усиления канала Х и коэффициента развертки слабым усилием повернуть по часовой стрелке до щелчка.
Измерение величины и длительности сигнала.
4.2.1. Зарисуйте полученную осциллограмму в масштабе 1:1 в бланке отчета. На рисунке покажите отрезки, соответствующие амплитуде сигнала (по оси Y) и периоду сигнала (по оси Х). Определите число делений N y и N x, соответствующих этим отрезкам.
4.2.2. Рассчитайте амплитуду сигнала A = C y N y и период сигнала T= C x N x, где C y – коэффициент усиления канала 1, C x – коэффициент развертки (определяются по положению переключателей «В/ДЕЛ» и «ВРЕМЯ/ДЕЛ»). Результаты расчета занесите в отчет.
ВЫВОД
В выводе укажите, для чего использовался осциллограф, как определялись параметры синусоидального напряжения с выхода генератора, запишите в стандартном виде полученные значения амплитуды, периода и частоты синусоидального напряжения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое гармонические колебания?
6.2. Запишите уравнение гармонических колебаний.
6.3. Что такое амплитуда колебаний?
6.4. Что такое частота колебаний, как связана с периодом колебаний?
6.5. Что такое период колебаний, как связан с частотой колебаний?
6.6. Что такое ЭЛТ, какие элементы содержит ЭЛТ7
6.7. Какой вид имеет осциллограмма синусоидального сигнала?
6.8. Как в работе определяется амплитуда синусоидального напряжения?
6.9. Как в работе определяется период синусоидального напряжения?
6.10. Как в работе определяется частота синусоидального напряжения?
Лабораторная работа №11.
Определение ускорения свободного падения при помощи маятника.
1. ЦЕЛЬ РАБОТЫ. Изучить гармонические колебания математического маятника. Определить ускорение свободного падения.
2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ. Тяжелый шарик на нити (математический маятник), штатив, рулетка, секундомер.
КРАТКАЯ ТЕОРИЯ
Математическим маятником называют материальную точку, подвешенную на нити. Хорошей моделью математического маятника является тяжелый маленький шарик, подвешенный на нити (рис.1). При отклонении от положения равновесия на небольшой угол шарик начинает совершать гармонические колебания и координата х шарика меняется со временем по гармоническому закону:
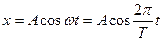 , (1)
, (1)
где А – амплитуда колебаний; ω – циклическая частота колебаний; Т – период колебаний. Период колебаний математического маятника определяется по формуле:
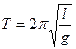 , (2)
, (2)
где l – длина математического маятника; g – ускорение свободного падения. Период колебаний Т можно определить экспериментально путем измерения времени одного колебания. Но время одного колебания мало – порядка одной, двух секунд, поэтому измерение без специальных приборов, «на глазок», будет не осень точным. Для увеличения точности измерения периода нужно измерить время t, за которое маятник совершает N колебаний, и рассчитать период по формуле:
 . (3)
. (3)
Измерив период Т идлину математического маятника l, можно рассчитать ускорение свободного падения:
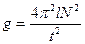 . (4)
. (4)
Относительная ошибка косвенного измерения:
 . (5)
. (5)
Мы считаем, что лабораторную работу будут выполнять люди серьезные и вряд ли ошибутся в подсчете числа N колебаний, поэтому принимаем ∆ N =0. В наших условиях проведения измерений абсолютная ошибка ∆ t определяется не столько ценой деления секундомера (ц.д.= 0.01с), сколько конечной скоростью нашей реакции при запуске и остановке секундомера. Поэтому принимаем ∆ t = 0,4 секунды.
РАБОЧЕЕ ЗАДАНИЕ
4.1. Используя штатив, подвесить стальной шарик на нити и измерить расстояние l от точки подвеса до центра шарика. Результат измерения и абсолютную ошибку ∆ l измерения записать в таблицу 1.
4.2. Отклонить нить от вертикали на небольшой угол и отпустить шарик. Математический маятник начнет совершать гармонические колебания.
4.3. В момент максимального отклонения шарика от положения равновесия запустить секундомер и остановить секундомер в момент, когда шарик совершит N =30 колебаний. Измеренное время t и абсолютную ошибку ∆ t записать в таблицу 1.
4.5. Используя формулы (4) и (5), рассчитать величину g и абсолютную ошибку ∆ g.
Таблица1.
| N | l | ∆ l | t | ∆ t | π | ∆ π |
| см | см | с | с | |||
ВЫВОД
В выводе указать, какой метод использовался для определения значения ускорения свободного падения, записать в стандартном виде полученное экспериментально значение g, табличное значение величины g, сравнить значения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое математический маятник? Что используется в данной лабораторной работе в качестве математического маятника?
6.2. Какие колебания совершает математический маятник, по какому закону меняется координата х маятника?
6.3. Что такое период колебаний математического маятника?
6.4. Как в работе определяется период колебаний математического маятника?
6.5. Как в работе определяется значение g ускорения свободного падения?
6.6. Как изменится период колебаний математического маятника, если длину нити увеличить в два раза?
6.7. Как изменится период колебаний математического маятника, если маятник поднять высоко в горы?
6.8. Как изменится период колебаний математического маятника, если маятник перенести на Луну?
6.9. Как изменится период колебаний математического маятника, если массу шарика увеличить в два раза?
6.10. Как изменится период колебаний математического маятника, если вместо стального шарика взять деревянный шарик такого же диаметра?
Лабораторная работа №12.






