1. ЦЕЛЬ РАБОТЫ. Приобретение навыков измерения линейных размеров твердых тел микрометром и штангенциркулем. Определение массы тела правильной геометрической формы различными методами. Научиться определять ошибки прямых и косвенных измерений, грамотно записывать результаты измерений.
2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ. Штангенциркуль, микрометр, весы, набор тел правильной геометрической формы.
3. КРАТКАЯ ТЕОРИЯ.
Масса – физическая величина, одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. Масса m, как мера инерции тела (называется инертной массой), определяется из основного закона движения классической механики Ньютона:
 , (1)
, (1)
где  - ускорение, которое приобретает тело под действием силы
- ускорение, которое приобретает тело под действием силы  .
.
В теории гравитации Ньютона каждое тело создает поле тяготения, пропорциональное массе тела. Посредством этого поля тела притягиваются друг к другу с силой, определяемой законом тяготения Ньютона:
 , (2)
, (2)
где r – расстояние между центрами масс взаимодействующих тел, G – универсальная гравитационная постоянная, m 1 и m 2 – массы тел. Масса, определяемая соотношением (2), называется гравитационной массой.
Опыт показал, что инертная и гравитационная массы численно равны друг другу. Этот фундаментальный закон природы называется принципом эквивалентности инертной и гравитационной массы. Этот принцип ниоткуда не следует, но экспериментально установлен с очень большой точностью. В классической физике считалось, что масса тела не изменяется ни в каких процессах (в релятивистской механике, рассматривающей движение тел с очень большими скоростями, сравнимыми со скоростью света с = 3 . 108м/с, масса тела зависит от скорости тела и называется релятивистской массой).
Массу тела можно измерить различными способами. Самым распространенным способом прямого измерения массы является взвешивание тела с помощью различных приборов (технические весы, аналитические весы, пружинные весы). В настоящей лабораторной работе предлагается измерить массу тела правильной геометрической формы путем взвешивания (прямое измерение) и путем расчета по формуле (косвенное измерение):
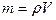 , (3)
, (3)
где ρ – плотность материала тела, V – объем тела.
Прежде чем приступить к выполнению лабораторной работы, необходимо внимательно ознакомиться с содержанием раздела «Введение Ошибки измерений», знать виды измерений (прямые, косвенные), методы расчета инструментальных ошибок, ошибок табличных величин, ошибок косвенных измерений, правила записи окончательного результата измерений.
Необходимо знать устройство и уметь пользоваться штангенциркулем и микрометром.
РАБОЧЕЕ ЗАДАНИЕ
4.1. Определение массы тела путем расчета по формуле.
4.1.1. Для выполнения рабочего задания получить у преподавателя или лаборанта тело правильной геометрической формы, штангенциркуль и микрометр. Далее, в качестве примера, дается подробное описание действий применительно к телу цилиндрической формы. Студент выполняет задание для заданного тела по приведенному примеру.
4.1.2. Сделать рисунок тела, на рисунке показать размеры, которые необходимо будет измерить для определения объема тела. Записать расчетную формулу для определения массы тела. Для циллиндрического тела: 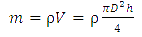 где где 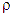 -плотность материала тела; V - обьём тела; D - диаметр цилиндра, измеряется микрометром; h - высота цилидра, измеряется штангельцуркулем. -плотность материала тела; V - обьём тела; D - диаметр цилиндра, измеряется микрометром; h - высота цилидра, измеряется штангельцуркулем.
| 
|
4.1.3. Подготовить таблицу для результатов измерений. В таблице предусмотреть место для записи инструментальной ошибки.
4.1.4. Провести необходимые измерения и результаты измерений записать в таблицу 1. В эту же таблицу записать значения табличных величин, необходимых для расчета массы, и их абсолютные ошибки; значения инструментальныx oшибок (см. раздел «Введение. Ошибки измерений»).
| Таблица 1 | |||||||||
| h | Δh | D | ΔD | 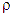
| Δ 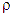
| π | Δπ | Δhи | ΔDи |
| мм | мм | мм | мм | г/см3 | г/см3 | мм | мм | ||
4.1.5. Рассчитать массу m тела, подставляя в расчетную формулу значения измеренных величин. Рассчитать абсолютную ошибку ∆ m. При подстановке в расчетную формулу величины выражаются в единицах одной и той же системы, например, СИ.
Для цилиндрического тела:
 ;
;  (4)
(4)
4.1.6. Записать результат измерений в стандартном виде: m=(m±Δm) [размерность].






