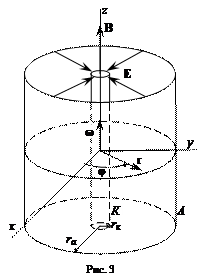
Рассмотрим теперь движение электрона в кольцевом пространстве, заключённом между цилиндрическим катодом К и коаксиальным с ним цилиндрическим анодом А двухэлектродной электронной лампы (рис. 3). Источником электронов служит катод, нагретый до высокой
температуры. Между катодом и анодом создаётся радиальное электрическое поле Е. Лампа помещена внутри соленоида, создающего однородное магнитное поле В, параллельное катоду. Такая конфигурация электрического и магнитного полей подобна конфигурации полей в магнетронах – генераторах мощных электромагнитных колебаний в области сверхвысоких частот (> 109Гц).
Первые эффективно работающие многорезонаторные магнетронные генераторы СВЧ были созданы в 1936–1937 гг. Н.Ф. Алексеевым и Д.Е. Маляровым. В настоящее время область их применения чрезвычайно широка – от мощных радиолокаторов до кухонных СВЧ печей.
Для описания траектории движения электронов в лампе воспользуемся цилиндрической системой координат. Положение электрона определяется расстоянием r от оси катода, полярным углом j и смещением z вдоль оси катода (рис.3). Вектор напряжённости электрического поля в цилиндрическом конденсаторе, образованном катодом и
и анодом лампы
Е = –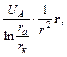 
(9)
где 
UA – разность потенциалов (напряжение) между анодом и катодом, ra – радиус анода, rк – радиус катода и r – расстояние от оси катода до исследуемой точки.
Вектор кулоновской силы, действующей на электрон, перпендикулярен катоду лампы и направлен по радиусу
F к = – е Е.
Сила Лоренца, действующая на электрон
F л = – e [ v, B ],
перпендикулярна вектору B индукции магнитного поля. Электроны, покидающие поверхность катода, под действием этих сил будут совершать движение по траекториям, лежащим в плоскостях (r, j), перпендикулярных оси z катода.
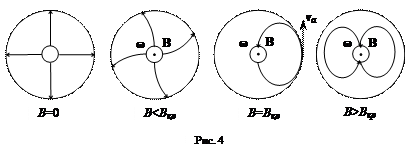
Траектории электронов в цилиндрическом магнетроне имеют сложную форму (рис.4). В отсутствие магнитного поля электроны движутся прямолинейно вдоль радиусов. В слабом поле траектории электронов несколько искривляются. При некотором критическом значении индукции магнитного поля Bкр траектории искривляются настолько, что только касаются анода. Наконец, при B>Bкр электроны не достигают анода и возвращаются на катод.
Как видно на рис.4, электрон одновременно участвует в двух видах движения: вдоль радиуса со скоростью
vr =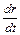 
и вращательном движении с угловой скоростью
w =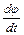 
.
Вектор ω параллелен вектору индукции магнитного поля B и направлен вдоль оси z введённой цилиндрической системы координат.
Для описания движения электрона в плоскости (r, j) используем основное уравнение динамики: скорость изменения момента импульса электрона равна моменту действующей на него силы:
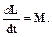(10)
Момент импульса электрона
L = J ω, (11)
где J=mr2 – момент инерции электрона относительно оси z. Момент силы, действующей на электрон
M =[ rF ]. (12)
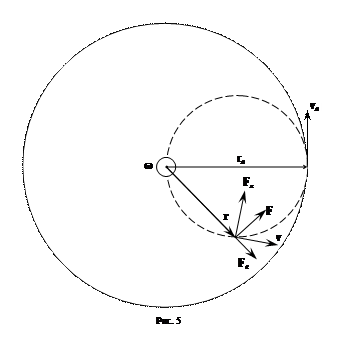
Сила F является равнодействующей сил Лоренца и Кулона (рис.5):
F = F л + F к = – e [ vB ] – e E. (13)
Подставим (13) в (12):
M = – e [ r [ vB ]] – e [ rE ].
Векторное произведение [ rE ] =0, так как векторы r и E параллельны.
Двойное векторное произведение преобразуем в соответствии с формулой [ a [ bc ]] = b (ac) – c (ab):
M = – e [ r [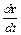 
B ]] = – e 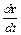(rB)+ e B (r 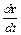). (14)
Первое скалярное произведение (rB) = 0, поскольку векторы r и B взаимно ортогональны. Подставим (11) и (14) в формулу (10)
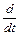(mr2 ω) = e B (r ).
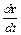Учитывая, что скалярное произведение
(r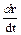 
) = 
= 
,
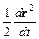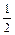
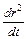получим:
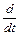(mr2 ω) =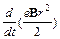 
или в проекции на ось z:
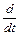(mr2w – 
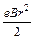) = 0.
Выражение в скобках является величиной постоянной, не зависящей от t:
mr2w – 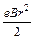= c. (15)
Постоянную интегрирования с найдём из начального условия: в момент вылета электрона с катода r=rк и w= 0:
c = –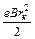 
.
Из (15) следует, что угловая скорость электрона возрастает по мере его удаления от катода
w =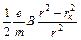 
. (16)
Для нахождения линейной скорости электрона v используем закон сохранения энергии. При перемещении от катода до точки с потенциалом U он приобретает скорость (см. выражение (1)):
v =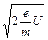 
(17)
(начальной скоростью электрона в момент его выхода из катода пренебрегаем, поскольку энергия теплового движения электронов при температуре катода Е ≈1000К составляет kT =1,38∙10-23Дж∙К-1∙1000К= =1,38∙10-20Дж ≈ 0,1эВ).
Теперь найдём критическое значение индукции магнитного поля Bкр. Скорость электрона в точке касания его траектории с поверхностью анода
vа = r 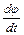= rawa. (18)
Подставляя в это уравнение выражения (16) и (17) и возведя в квадрат, получим:
2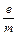 
Ua = (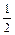 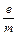Bкр 
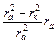)2.
Отсюда:
= 
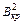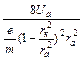. (19)
Формула (19) позволяет вычислять величину отношения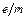 
, если при заданном Ua найдено такое значение магнитного поля Bкр (или, наоборот, при заданном B такое значение Uaкр), при котором электроны перестают попадать на анод:
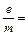
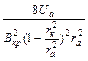. (20)
Характеристика магнетрона, показывающая зависимость анодного тока от индукции магнитного поля в идеальном случае имеет вид,
 |
показанный на рис.6 пунктирной линией. При B<Bкр все электроны без исключения попадают на анод, величина тока Ia постоянна и не зависит от B. При B>Bкр все электроны возвращаются на катод, не достигнув поверхности анода.
В реальной лампе невозможно обеспечить полную коаксиальность анода и катода, а также идеальную однородность электрического поля и параллельность вектора индукции магнитного поля с осью катода. Кроме того, электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Распределение скоростей теплового движения электронов, также как и молекул газа, примерно подчиняется закону распределения Максвелла. Все эти причины при- водят к тому, что практически получаемые характеристики Ia = Ia(B)
(сплошная линия на рис.6) не имеют такой крутой падающей части, как у идеальной характеристики.
