Свободные колебания в контуре без активного сопротивления

Содержание

 

1. Цель работы …………………………………………………………..4

2. Теоретическая часть…………………………………………………..4

2.1. Свободные колебания в контуре без активного

сопротивления…………………………………………………...4

2.2. Свободные затухающие колебания…………………………….7

3. Приборы и оборудование……………………………………………10

4. Требования к технике безопасности………………………………..11

5. Порядок выполнения работы………………………………………..11

6. Требования к отчету…………………………………………………13

7. Контрольные вопросы……………………………………………….14

Список литературы………………………………………………….14

 

 

Лабораторная работа № 48

Исследование затухающих колебаний

В колебательном контуре

Цель работы

Изучение параметров и характеристик колебательного контура.

 

 

Теоретическая часть

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи, напряжения) изменяются периодически. Электромагнитные колебания могут возникнуть в цепи, содержащей индуктивность L и емкость С. Такая цепь называется колебательным контуром. Токи в колебательном контуре являются квазистационарными, то есть в каждый момент времени сила тока во всех сечениях одинакова. Мгновенные значения квазистационарных токов подчиняются закону Ома и вытекающим из него законам Кирхгофа.

 

 

Свободные колебания в контуре без активного сопротивления

Примером электрической цепи, в которой могут возникнуть свободные электрические колебания, является простейший колебательный контур, состоящий из конденсатора электроемкостью С и соединенной с ним последовательно катушки индуктивности L. На рисунке 2.1 изображены последовательные стадии колебательного процесса в этом контуре. Если присоединить отключенный от индуктивности конденсатор к источнику напряжения, на обкладках конденсатора появляются разноименные заряды + q ₀ и – q ₀ (стадия 1). Между обкладками возникает электрическое поле, энергия которого равна 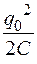. Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, конденсатор начнет разряжаться и в контуре потечет ток I. В результате энергия электрического поля будет уменьшаться, но возрастает энергия магнитного поля, обусловленного током, текущим через индуктивность. Эта энергия равна .

 

 

 

 

Рис. 2.1

 

Поскольку активное сопротивление контура равно нулю, полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и остается постоянной. Поэтому в момент времени , когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, энергия магнитного поля, а следовательно, и ток достигает наибольшего значения I ₀ (стадия 2). Начиная с этого момента, ток в контуре будет убывать, в связи с этим начнет ослабевать магнитное поле катушки, в ней индуцируется ток, который течет в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который через время обратится в нуль, а заряд достигнет первоначального значения q ₀ (стадия 3). Затем те же процессы протекают в обратном направлении (стадии 4, 5), после чего система приходит в исходное состояние (стадия 5) и весь цикл повторяется снова и снова. В ходе процесса изменяются периодически заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.

Получим уравнение колебаний в контуре без активного сопротивления (рисунок 2.2).

 

Рис. 2.2

 

Закон Ома для цепи 1 – 3 – 2 имеет вид

, (2.1)

или , (2.2)

где q и φ₁ – φ₂ = – – заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; – э.д.с. самоиндукции в катушке.

Из закона сохранения заряда следует, что сила квазистационарного тока в контуре . Перейдя в уравнении (2.2) от силы тока I к заряду q и введя обозначение

, (2.3)

получаем дифференциальное уравнение свободных колебаний в контуре без активного сопротивления

, (2.4)

где ω₀ – собственная частота контура. Решением этого уравнения является выражение

, (2.5)

где φ – начальная фаза колебаний.

Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с собственной частотой ω₀.

Период колебаний в контуре определяется формулой Томсона

. (2.6)

Разность потенциалов обкладок конденсатора (напряжение) отличается от заряда множителем 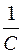и совпадает по фазе с зарядом q:

. (2.7)

Продифференцировав формулу (2.5) по времени, получим выражение для силы тока в контуре

. (2.8)

Таким образом, сила тока опережает по фазе заряд конденсатора на .

Энергия электрического поля конденсатора W _э и энергия магнитного поля катушки W _м соответственно равны

(2.9)

,

.

Колебания, происходящие в электрическом колебательном контуре, часто называют электромагнитными колебаниями.

Полная энергия электромагнитных колебаний в контуре не изменяется с течением времени и равняется сумме энергий электрического и магнитного полей

. (2.10)