Метод измерений и описание установки.

Федеральное агентство по образованию Российской Федерации

Филиал государственного образовательного учреждения

Высшего профессионального образования

«Московский энергетический институт

(технический университет)»

В г. Волжском

 

Кафедра: Общая физика

 

 

Лабораторная работа №25

«Вынужденные электромагнитные колебания»

 

Работу выполнил:

студент группы ЭОП-09 В

Шамьянов С.А.

 

Проверил преподаватель:

Мельников В.П.

 

 

Волжский 2010

 

ЦЕЛЬ РАБОТЫ

Определение зависимости силы тока в колебательном контуре от частоты вы­нуждающей ЭДС. Построение резонансных кривых

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Рассмотрим процессы, протекающие в колебательном контуре (рис.1), присоединённому к внешнему источнику, ЭДС которого изменяется по гармоническому закону

 

 

Обозначим через U напряжение на конденсаторе, а через I – ток в контуре. Согласно второму правилу Кирхгофа сумма напряжений на элементах цепи равна алгебраической сумме ЭДС в контуре:

 

, (2.1)

где – ЭДС самоиндукции, возникающей в катушке с индуктивностью L при прохождении в ней переменного тока.

 

Уравнение (2.1) можно записать в виде

(2.2)

 

Выразим напряжение в конденсаторе через ток:

 

 

Здесь q – заряд на конденсаторе. Подставляя в (2.2) найденное значение напряжения, получим:

 

 

Продифференцируем это выражение по t:

 

(2.3)

 

Далее будем использовать обозначения, введённые в лабораторной работе №24. Тогда (2.3) примет вид:

 

(2.4)

Полученное уравнение является линейным неоднородным (, ) дифференциальным уравнением второго порядка.

Уравнения типа (2.4) описывают поведение широкого класса колебательных систем (электрических, механических и т.п.) под влиянием внешнего гармонического воздействия.

Через некоторое время после включения гармонически изменяющейся ЭДС (), которое потребуется для полного затухания собственных колебаний, в колебательном контуре устанавливается переменный ток с частотой, равной частоте вынуждающей ЭДС.

Установившиеся колебания в контуре, независимые от начальных условий, определяются частным решением уравнения (2.4), которое имеет вид

 

(2.5)

 

Здесь - амплитудное значение силы тока, - угол сдвига фаз между внешней ЭДС и током в цепи.

Подставив (2.5) в (2.4) найдём значения и :

 

(2.6)

 

(2.7)

 

где (2.8)

 

Формула (2.6), показывающая зависимость амплитуды переменного тока в колебательном контуре от амплитуды вынуждающей ЭДС, аналогична закону Ома для замкнутой цепи постоянного тока. Поэтому величина z называется полным сопротивлением электрической цепи переменного тока (колебательного контура). Оно складывается из активного (омического) сопротивления R, индуктивного сопротивления и емкостного сопротивления . Как видно из (2.6) амплитуда силы тока в контуре достигает максимального значения при минимальном значении z, т.е. при . При этом полное сопротивление контура минимально и равно его активному сопротивлению. В этом случае 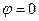, т.е. сила тока совпадает по фазе с вынуждающей ЭДС и равна

(2.9)

 

При постоянных значениях L, C независимо от величины активного сопротивления контура, амплитуда силы тока достигает максимального значения при одном и том же значении - циклической частоты вынуждающей ЭДС, называемой резонансной, равной

 

(2.10)

где - собственная циклическая частота колебательного контура.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей ЭДС к частоте, равной или близкой собственной частоте колебательного контура называется резонансом.

 

Графическая зависимость амплитуды тока от частоты вынуждающей ЭДС называется резонансной кривой. Чем меньше активное сопротивление контура, тем больше амплитуда силы тока при резонансе и ярче выражена резонансная кривая.

Добротностью контура Q при называют соотношение

(2.11)

здесь - ширина резонансной кривой на высоте .

Из (2.11) следует, что чем «острее» резонансная кривая, тем больше добротность контура.

 

МЕТОД ИЗМЕРЕНИЙ И ОПИСАНИЕ УСТАНОВКИ.

 

Принципиальная схема установки изображена на рис. 3.

 

	Рис.3.

 

 

PQ – генератор импульсов ГЗ-118;

М – модуль (колебательный контур);

PV – вольтметр В7-38.

 

 

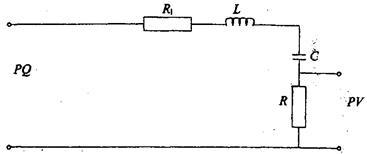Электрическая схема модуля М показана на рис. 4.

 

 

	Рис.4.

 

С выхода генератора звуковых сигналов PQ на вход модуля М подается выну­ждающая ЭДС, изменяющаяся по гармоническому закону.

Для снятия резонансной кривой I₀ = f(w) к гнездам PV модуля М подключается вольтметр. Измеряется напряжение U₀ на сопротивлении R (ток I в контуре меня­ется синхронно с этим напряжением) при различных частотах n, задаваемых зву­ковым генератором.