Лабораторная работа №16
методом электрогидродинамической аналогии (ЭГДА)
Общие сведения о методе аналогий.
Известно, что совершенно различные по своей физической природе движения материальных тел иногда могут описываться одинаковыми по форме уравнениями. Тогда говорят, что имеет место аналогия сопоставляемых явлений. При этом обычно удается установить характерные величины (параметры), соответствующие друг другу в этих процессах, то есть установить аналоговые соотношения. Тогда, если в процессе 1 определение какого-либо параметра А1 затруднено, то можно найти подобный ему параметр А2 в процессе 2 и с помощью аналогового соотношения пересчитать на А1.
Для этого необходимо, чтобы:
· сопоставляемые явления описывались одинаковыми дифференциальными уравнениями (имели аналоговое соотношение);
· процессы имели идентичные граничные условия.
Существуют различные виды аналогий. В данной работе рассматривается электрогидродинамическая аналогия (ЭГДА) – аналогия, между течением электрического тока в плоском проводнике и плоским потенциальным потоком несжимаемой жидкости.
Плоским называется течение, для которого декартовую систему координат можно выбрать так, чтобы одна из компонент скорости всюду равнялась нулю.
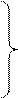 Известно, что для плоских потоков существует функция тока
Известно, что для плоских потоков существует функция тока 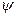 , а если это течение потенциально (отсутствие вихрей), то и потенциал скорости
, а если это течение потенциально (отсутствие вихрей), то и потенциал скорости  , которые могут быть записаны в следующем виде через проекции скоростей
, которые могут быть записаны в следующем виде через проекции скоростей 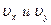 :
:
 (16.1)
(16.1)
Причем:
 .
.
Кроме того, для любого течения должно выполняться уравнение неразрывности, которое для установившегося плоского потока несжимаемой жидкости имеет вид:  то есть:
то есть:
 (16.2)
(16.2)
Из уравнений (16.1) и (16.2) получим уравнения Лапласа:
 |
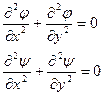 (16.3)
(16.3)
Гидродинамическая сетка.
Задача об обтекании тела потенциальным потоком сводится к решению одного из уравнений системы (16.3) при определенных граничных условиях. Аналитическое решение этих уравнений при произвольных граничных условиях достаточно сложно. Поэтому используется графический метод решения, основанный на построении гидродинамической сетки.
Гидродинамической сетка представляет собой изображение семейства линий тока 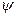 = const и ортогональных к ним семейства эквипотенциалей
= const и ортогональных к ним семейства эквипотенциалей  = const (линий равного потенциала).
= const (линий равного потенциала).
Основные свойства сетки:
· ортогональность (линии тока перпендикулярны эквипотенциалям);
· ни одна из линий сетки не может начинаться или заканчиваться внутри области течения. Каждая из них либо начинается и заканчивается на границе области течения, либо представляет собой замкнутую кривую;
· одноименные линии тока не могут пересекаться нигде, кроме особых и критических точек, то есть точек, в которых скорость равна соответственно нулю или бесконечности;
· сетка в малом квадратична ( ), см. рис.16.1;
), см. рис.16.1;
· расход между двумя линиями тока постоянен и равен разности значений функций тока на этих линиях:
 , (16.4) где
, (16.4) где  - расстояния по эквипотенциалям между выбранными линиями тока соответственно на бесконечности и в окрестности интересующей точки (рис. 16.1).
- расстояния по эквипотенциалям между выбранными линиями тока соответственно на бесконечности и в окрестности интересующей точки (рис. 16.1).
- гидродинамическая сетка обратима, то есть каждой сетке соответствуют два возможных течения таких, что эквипотенциали одного служат линиями тока другого и наоборот.

Рис. 16.1. Обтекание круглого цилиндра потенциальным потоком
Из уравнения (16.4) имеем:
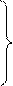 где
где  - коэффициент скорости:
- коэффициент скорости:  (16.5)
(16.5)
Используя уравнение Бернулли можно определить коэффициент давления:
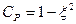 . (16.6)
. (16.6)
Как было отмечено выше, метод ЭГДА представляет собой аналогию между движением электрического тока в плоском проводнике и плоским потенциальным течением несжимаемой жидкости.
В данной лабораторной работе в качестве плоского проводника тока используется электропроводящая бумага, а обтекаемое тело представляет собой металлический цилиндр. Создавая на электрической модели такие же граничные условия, как и для моделируемого потока жидкости, можно получить идентичную для обоих течений картину пересечения линий тока и эквипотенциалей, то есть гидродинамическую сетку.
В качестве характерных параметров моделируемого течения выступают функция тока 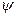 и потенциал скорости потока
и потенциал скорости потока  . Можно доказать, что математической моделью
. Можно доказать, что математической моделью  или
или  может служить электрический потенциал W.
может служить электрический потенциал W.
Укажем некоторые из основных преимуществ метода ЭГДА:
· изготовление электрической модели значительно проще, чем создание физической модели течения жидкости;
· измерение электрических параметров в плоском проводнике (аналоге области течения жидкости) осуществить легче и точнее, чем непосредственные измерения параметров в потоке жидкости.
Проведение эксперимента (построение гидродинамической сетки).
Из электропроводной бумаги вырезается область течения (прямоугольник) так, чтобы его стороны с достаточной степенью точности можно было принять попарно за линии тока и эквипотенциали.
Далее необходимо удовлетворить граничным условиям. Обычно при построении сетки требуется осуществить два вида условий:
- для эквипотенциалей:  , (16.7)
, (16.7)
- для линий тока:  (16.8)
(16.8)
Здесь n – направление, перпендикулярное соответственно эквипотенциалям и линиям тока.
Эти два граничных условия на электрической модели сводятся к следующему условию для электрического потенциала:
W= const,  . (16.9)
. (16.9)
Условие (16.9) необходимо осуществить при проведении опыта.
Обеспечение условия W= const выполняется путем наложения металлических шин на электропроводную бумагу. Таким образом, создается граница течения тока, проводимость которой значительно выше проводимости области течения, что и позволяет считать потенциал на шинах неизменным.
Условие  равносильно требованию отсутствия нормальной составляющей тока на границе, то есть граница должна быть непроницаема для тока. Это достигается за счет обреза области течения вдоль непроницаемой границы.
равносильно требованию отсутствия нормальной составляющей тока на границе, то есть граница должна быть непроницаема для тока. Это достигается за счет обреза области течения вдоль непроницаемой границы.
Отличие процессов снятия линий тока и эквипотенциалей заключается только в различном расположении шин и присутствии или отсутствии (вырезе) обтекаемого тела. При этом всегда щупом ищутся точки с равным электрическим потенциалом.
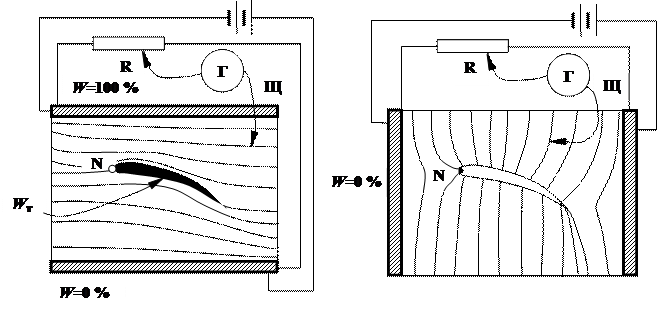
а) Построение линий тока. Для построения линий тока шины располагаются, как показано на рис. 16.2 (а), на которых устанавливаются потенциалы условно равные соответственно W= 0% и W= 100% (абсолютные значения потенциалов значения не имеют).
Контур обтекаемого тела является одной из линий тока, т. е линией равного электрического потенциала. Поэтому контур, также как и шины, должен быть хорошо проводящим, чтобы электрический потенциал на нем был везде одинаков. Практически это условие может быть реализовано наклейкой электропроводным клеем профиля, вырезанного из металлической фольги (или нанесением контура сплавом Вуда), либо размещением на электропроводной бумаге металлического тела требуемого профиля (в данном случае металлического цилиндра). При подаче на шины разности потенциалов на контуре устанавливается некоторое значение электрического потенциала W Т, характеризующее линию тока, проходящую через одну из критических точек (например, точку N). На плоском проводнике всегда можно найти ряд точек, потенциал которых равен заданному W Т. Для этого игла щупа Щ перемещается по области течения (электропроводной бумаге) до тех пор, пока гальванометр Г не покажет значение тока, равное нулю. В итоге получается ряд точек одинакового электрического потенциала, то есть критическая линия тока. Остальные линии тока строятся аналогичным образом с шагом 5%–10%, отсчитывая от обтекаемого тела в обе стороны. В результате имеем семейство линий тока.
б) Построение эквипотенциалей. Электропроводная бумага освобождается от шин и на ней вырезается отверстие по контуру обтекаемого тела (рис.16.2, (б)). Вырез делается для обеспечения условия электрической непроводимости контура тела. Затем накладываются шины на стороны, противоположные случаю а). Игла щупа Щ помещается в критическую точку N и строится проходящая через нее эквипотенциаль. С шагом 5%–10 % строятся и другие эквипотенциали, образуя в итоге семейство эквипотенциалей.
 Следует помнить, что при построении линий тока и эквипотенциалей шаги должны быть одинаковыми.
Следует помнить, что при построении линий тока и эквипотенциалей шаги должны быть одинаковыми.
| |||||
| |||||
| |||||
Рис. 16.2. Построение линий тока (а) и эквипотенциалей (б)
Обработка результатов измерений.
1. Перенести гидродинамическую сетку на обычную бумагу.
2. Пронумеровать точки по контуру тела. По линейке измерить расстояния между линиями тока на бесконечности  и вблизи контура тела
и вблизи контура тела 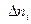 .
.
3. Рассчитать значения коэффициентов скорости  и давления CP, а также построить графики их распределения по контуру тела. Для эквипотенциали в срединной части профиля и эквипотенциали, проходящей или находящейся вблизи критической точки рассчитать и построить графики коэффициента скорости
и давления CP, а также построить графики их распределения по контуру тела. Для эквипотенциали в срединной части профиля и эквипотенциали, проходящей или находящейся вблизи критической точки рассчитать и построить графики коэффициента скорости  .
.






