Плоская антенная решетка, множитель решетки и его анализ.

Линейные АР позволяют сформировать направленное излучение только в одной плоскости, проходящей через ось решетки. Плоские антенные решетки кон-центрируют излучение в двух плоскостях, т.е. создают в пространстве ДН с узким главным лепестком.

Форма плоской АР может быть прямоугольной, круглой, шестиугольной и определяется как требованиями, предъявляемыми к форме ДН, так и конструктив-ными особенностями системы. Излучатели в плоских АР располагаются в узлах прямоугольной или треугольной сетки, как это показано на рисунке.

а) б)

а - АР с прямоугольной сеткой; б - АР с треугольной сеткой.

Применение излучателей, расположенных в узлах треугольной сетки, явля-ется более предпочтительным, т.к. позволяет увеличить расстояние между сосед-ними излучателями, а, следовательно, уменьшить их взаимное влияние друг на друга и вероятность появления паразитных интерференционных главных макси-мумов высших порядков.

Множитель плоской АР и его анализ. Условие формирования одного глав-ного лепестка.

Множитель плоской АР.

Рассмотрим эквидистантную равноамплитудную линейно-фазную решетку, расположенную в плоскости XOY, как это показано на рисунке.

а) б)

Пусть N_x и N_y - число излучателей в столбцах и рядах; d_x и d_y – расстоя-ние между соседними излучателями по осям OX и OY соответственно; q_x и q_y – углы, отсчитываемые на точку наблюдения соответственно от осей OX и OY.

Каждый столбец излучателей (столбец будем считать состоит из излучате-лей, расположенных вдоль оси OX) представляет собой прямолинейную эквидис-тантную равноамплитудную линейно-фазную антенную решетку.

Множитель такой АР, как было установлено ранее, можно записать в виде:

. (15)

Если произвести эквивалентную замену каждого столбца плоской АР на одиночный гипотетический излучатель, с собственной ДН, совпадающей с выра-жением (15), то получим также линейную решетку, но ориентированную вдоль оси OY:

В соответствии с теоремой перемножения диаграмм направленности, можем записать:

, (16)

где F_O(q_x) – ДН гипотетического излучателя, представляющая собой выра-жение (15), а F_С_y(q_y) – множитель антенной решетки, состоящей из гипотетичес-ких излучателей. Его можно найти по выражению:

. (17)

Введем обозначения обобщенных угловых координат:

. (18)

Подставляя (18) в (15) и (17), можем получить выражение для множителя плоской АР:

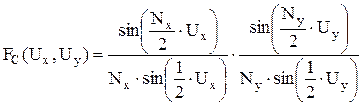. (19)

В сферической системе координат множитель АР является функцией углов q и j, а не q_x и q_y. Определим связь между ними. Заметим, что cosq_x и cosq_y есть проекции единичного вектора 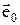, ориентированного в направлении точки наблю-дения на оси OX и OY соответственно, как это показано на рисунке:

. (20)

С другой стороны, учитывая известную взаимосвязь между прямоугольной и сфе-рической системами координат, проекции единичного вектора можно выразить через углы q и j:

. (21)

Тогда, подставляя (21) в (20), и с учетом (18), можем из (19) получить оконча-тельное выражение для множителя плоской АР в сферической системе координат:

. (22)

Из выражения (22) легко видеть, что в главных плоскостях XOZ (j = 0) и YOZ (j = p/2) сечение пространственной ДН плоской АР совпадает с формой ДН линейных АР.

Анализ множителя плоской антенной решетки.

Анализируя выражение (22), приходим к следующим выводам:

- множитель плоской АР представляет собой произведение множителей двух линейных АР; первая из них представлена излучателями, образующими столбец, вторая - строку;

- анализ множителя плоской АР изначально сводится к анализу множителей линейных АР, который можно производить совершенно независимо друг от друга.

Поэтому, дополнительно для плоской АР нас будут интересовать направление главного лепестка и управление им в пространстве.

Условия существования одного главного лепестка.

Направление (углы) главных лепестков ДН можно определить, исходя из выражений для соответствующих линейных АР:

(23)

Из этого следует вывод, что управление положением главного лепестка плоской АР (m_x = 0; m_y =0) независимо можно осуществлять, изменяя величины фазовых сдвигов токов возбуждения в элементах строки и столбца. При этом, естественно, происходит отклонение главного лепестка либо от оси OX, либо от оси OY.

Для того, чтобы плоская АР имела только один главный лепесток, необходимо, чтобы каждая линейная АР (образующая строку или столбец) имела бы только один главный лепесток, т.е. чтобы выполнялись неравенства:

. (24)

Так как каждый множитель линейной АР в пространстве представляет собой конус вращения (коническую воронку), ось которого совпадает с соответствующей осью решетки, то для существования в множителе плоской АР только одного главного лепестка нулевого порядка необходимо пересечение в прост-ранстве данных конусов. При этом главные лепестки результирующей ДН фор-мируются в тех направлениях, в которых пересекаются оба конуса, как это показано на рисунке:

Это будет, если выполняется условие: . Очевидно, что таких направлений будет два. Но так как реально плоскостные АР имеют односто-роннюю направленность, то фактически создается лишь один главный лепесток. Если неравенство (24) не выполняются, то будет взаимное пересечение главного лепестка одной АР с боковыми другой. При этом отсутствует направление преи-мущественного излучения энергии.

3. Антенные решетки с неравномерным амплитудным распределением. Понятие об оптимальных ДН.

До сих пор рассматривались АР с равномерным распределением амплитуды тока излучателей. Однако на практике они находят малое применение, т.к. соз-дают ДН с сравнительно высоким уровнем боковых лепестков (η_бл = 21 %). Поэтому для практики представляет большой интерес выбор рационального вида амплитудного распределения тока вдоль антенной решетки. С этой целью приме-няют спадающие к краям, симметричные относительно центра, виды амплитудных распределений, как это показано на рисунке:

Следует заметить, что множитель такой АР определяется по более общему выражению, рассмотренному нами вначале предыдущей лекции. Анализ показы-вает, что чем сильнее спадает к краям антенной системы амплитуда тока, тем главный лепесток шире, но уровень боковых лепестков меньше. В специальной литературе приведены виды амплитудных распределений и выражения для множителей антенных решеток с этими видами амплитудных распределений, а также формулы для расчета ширины множителей и уровня боковых лепестков.

Иногда требуется применение оптимальных амплитудных распределений, при которых:

уровень боковых лепестков является минимальным для заданной ширины ДН;

ширина ДН является минимальной для заданного уровня боковых лепест-ков.

В теории антенн показано, что при таком амплитудном распределении мно-житель АР должен быть представлен в виде полинома Чебышева, причем степень полинома равна числу элементов в линейной АР.

Оптимальность ДН в указанном смысле обеспечивается тем, что полином Чебышева наименее уклоняется от нуля на отрезке, соответствующем действи-тельным углам, т.е. множитель, описываемый таким полиномом будет иметь наи-меньший уровень боковых лепестков. Расчет амплитудных распределений по из-вестной конструкции АР и предъявляемым исходным требованиям приведен в специальной литературе.