Определить размах варьирования случайной величины и составить вариационный ряд распределения.
По формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд.
3. Найти выборочную среднюю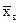 
, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение sв, моду Мо, медиану Ме;и коэффициент вариации dв.
4. Построить эмпирическую функцию распределения вероятностей F*(x).
Задание № 2. По данным предыдущего задания необходимо:
1. Построить гистограмму относительных частот и линию эмпирической плотности.
2. Пользуясь критерием Пирсона проверить гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости a=0,05, предварительно вычислив для каждого интервала группирования вариационного ряда выравнивающие частоты.
3. На гистограмме относительных частот нанести линию теоретической плотности f(x) нормального распределения.
4. найти доверительный интервал для оценки неизвестного математического ожидания генеральной совокупности случайной величины с надежностью 0,95.
Задание № 3. Для двумерной случайной величины (Х, У), представленной в корреляционной таблице, необходимо:
1. Определить выборочный коэффициент корреляции rв;
2. Установить его значимость при доверительной вероятности g=0,95 (уровне значимости a =1-g =0,05);
3. В случае линейной корреляции между СВ Х и У найти выборочное уравнение прямой 
регрессии У на Х;
4. На корреляционном поле парных зависимостей СВ Х и У нанести полученное уравнение прямой регрессии.
| х у | ny | ||||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
Контрольная работа
Вариант 2.
Задание № 1.Для заданной выборки из генеральной совокупности СВ Х (n=100) необходимо:
Определить размах варьирования случайной величины и составить вариационный ряд распределения.
По формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд.
3. Найти выборочную среднюю 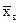, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение sв, моду Мо, медиану Ме;и коэффициент вариации dв.
4. Построить эмпирическую функцию распределения вероятностей F*(x).
Задание № 2. По данным предыдущего задания необходимо:
1. Построить гистограмму относительных частот и линию эмпирической плотности.
2. Пользуясь критерием Пирсона проверить гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости a=0,05, предварительно вычислив для каждого интервала группирования вариационного ряда выравнивающие частоты.
3. На гистограмме относительных частот нанести линию теоретической плотности f(x) нормального распределения.
4. найти доверительный интервал для оценки неизвестного математического ожидания генеральной совокупности случайной величины с надежностью 0,95.
Задание № 3. Для двумерной случайной величины (Х, У), представленной в корреляционной таблице, необходимо:
1. Определить выборочный коэффициент корреляции rв;
2. Установить его значимость при доверительной вероятности g=0,95 (уровне значимости a =1-g =0,05);
3. В случае линейной корреляции между СВ Х и У найти выборочное уравнение прямой регрессии У на Х;
4. На корреляционном поле парных зависимостей СВ Х и У нанести полученное уравнение прямой регрессии.
| х у | ny | ||||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | ||||||
| - | - | - | |||||
| - | - | - | |||||
| nx | n=100 |
Контрольная работа
Вариант 3.
Задание № 1.Для заданной выборки из генеральной совокупности СВ Х (n=100) необходимо:
