ЭКЗАМЕНАЦИОННЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ
1. Чему равен результат следующих действий со случайными событиями
а) 
б) 
в) 
г) 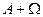
д) 
е) 
ё) 
ж) 
з) 
и) 
2. Событие А: «При бросании кубика выпадает чётное число очков».
Событие В: «При бросании кубика выпадает 5 очков».
Определить вероятность события А+В?
Определить вероятность события А×В?
3. Событие А: «При бросании кубика выпадает чётное число очков».
Событие В: «При бросании кубика выпадает не более 2 очков».
Определить вероятность события А–В?
Определить вероятность события А+В?
4. Вдоль государственной границы пограничные заставы расположены в следующем порядке: А, Б, В, и Г.
Достоверно известно, что будет предпринята попытка незаконного пересечения границы между заставами А и Г.
Вероятность пересечения на участке от А до В – 0,7.
Вероятность пересечения на участке от Б до Г – 0,6.
Определить вероятность того, что попытка пересечения границы будет предпринята на участке от Б до В.
5. Два наблюдателя независимо друг от друга ожидают появления объекта, находясь в разных местах.
Вероятность того, что первый наблюдатель не пропустит появление объекта – 0,9.
Вероятность того, что второй наблюдатель не пропустит появление объекта – 0,8.
Определить вероятности следующих событий
а) первый наблюдатель пропустит появление объекта
б) оба наблюдателя не пропустят появление объекта
в) оба наблюдателя пропустят появление объекта
г) первый наблюдатель пропустит, а второй не пропустит появление объекта
д) первый наблюдатель не пропустит, а второй пропустит появление объекта
е) появление объекта не пропустит ровно один наблюдатель
ё) появление объекта не пропустит хотя бы один наблюдатель (т.е. не менее одного)
6. Наблюдатель следит за одинаковыми объектами, появляющимися последовательно один за другим, в сложных условиях наблюдения; результаты наблюдений независимы друг от друга.
Вероятность того, что наблюдатель не пропустит появление объекта – 0,8.
Определить вероятности следующих событий
а) при появлении трёх объектов наблюдатель пропустит первый, а два следующие заметит
б) при появлении четырёх объектов наблюдатель пропустит первые три, а последний заметит
7. Определить по графику закона распределения случайной величины X вероятности следующих событий

а) X < 2,5
б) X > 5
в) 4 £ X < 20
г) 5 < X < 7
8. По графику плотности распределения случайной величины X определить вероятности следующих событий
 |
а) X < 3
б) X > 6
в) 5 < X < 7
г) 1 < X < 10
9. Чему равна цена деления по оси ординат для следующей плотности распределения? Какова единица измерения величины,откладываемой по вертикальной оси, если единица измерения по горизонтальной оси – год.
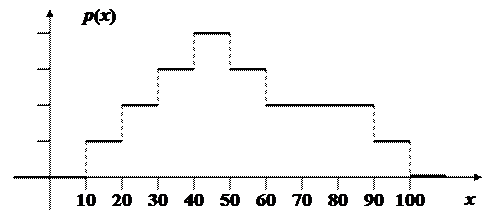 |
10. Чему равна цена деления по оси абсцисс для следующей плотности распределения? Какова единица измерения величины откладываемой по горизонтальной оси, если единица измерения по вертикальной оси – 1/(чел.×ч).
 |
11. Закон распределения задан таблицей
xi 0 100 200
P(xi) 0,8 0,1 0,1
Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение
12. Нормально распределённая случайная величина задана уравнением плотности распределения.
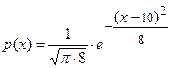
Указать математическое ожидание, дисперсию и среднеквадратическое отклонение.
Нарисовать график плотности распределения.
13. Закон распределения задан графически.
 |
Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение
 |
14. Дан график плотности нормального распределения
Оценить математическое ожидание, среднеквадратическое отклонение и дисперсию случайной величины.
Тема. Выборочный метод
15. В результате 100 опытов с дискретной случайной величиной получены следующие результаты появления её различных значений
2,0 – 30 раз
4,0 – 40 раз
6,0 – 20 раз
8,0 – 10 раз
Вычислить частоты различных значений.
Вычислить выборочное среднее.
16. Даны выборочные значения:
3, 7, -1, 1, 9, -3, 5.
Вычислить:
выборочное среднее,
выборочную дисперсию,
выборочное среднеквадратическое отклонение.
17. Даны выборочные значения:
8, 3, 8, -2, -2.
Вычислить:
выборочное среднее,
выборочную дисперсию,
выборочное среднеквадратическое отклонение оценки математического ожидания,
доверительный интервал для оценки математического ожидания по двукратной ошибке.
18. Имеется выборка объёмом 100.
По ней рассчитаны оценки математического ожидания и дисперсии случайной величины: 435 и 1600, соответственно.
Вычислить:
среднеквадратическую ошибку оценки,
доверительный интервал для оценки математического ожидания по однократной ошибке
19. По выборке небольшого объёма сделаны оценки математического ожидания и дисперсии случайной величины, которые составляют соответственно 25 и 75.
Вычислить необходимый объём выборки, обеспечивающий относительную ошибку оценки математического ожидания, равную 2 %.
20. Дана таблица с парами данных
x: 1 3 1 3 3 3 1 1
y: 2 7 2 7 2 2 7 7
Определить коэффициент корреляции
21. Дана таблица с парами данных
x: 1 2 3 4 1 2 3 4
y: 8 7 6 5 8 7 6 5
Определить коэффициент корреляции
22. Дана таблица с парами данных
x: 1 2 3 4 1 2 3 4
y: 5 6 7 8 5 6 7 8
Определить коэффициент корреляции
23. С помощью программы Эксель смоделировать 20 выборочных значений равномерно распределённой случайной величины в пределах от 10 до 22 и с помощью встроенных функций Эксель вычислить оценки среднего, дисперсии. Рассчитать по формулам истинные значения и сравнить со значениями оценок.
24. С помощью программы Эксель смоделировать две независимые выборки по 10 значений каждая равномерно распределённой случайной величины, построить точечную диаграмму по парам значений из обеих выборок и с помощью встроенной функции Эксель вычислить оценку коэффициента корреляции. Сравнить с истинным значением.
25. В тире стрелок выполнил 5 выстрелов по мишени из винтовки, а затем снял мишень со стены. В стене осталось 5 свежих пулевых отверстий. Координаты отверстий (x см – от пола; y см – от левого угла тира) таковы: (152; 310), (161; 306), (150; 312), (160; 309), (157; 303). Оцените координаты центра, которые имела мишень на стене, по координатам отверстий, в предположении, что мушка у винтовки не сбита и пристреляна «по центру».
26. По выборке небольшого объёма сделаны оценка доли двузначного качественного признака в генеральной совокупности: 0,8. Требуется оценить объём выборки, необходимый, чтобы среднеквадратическая ошибка оценки доли качественного признака не превышала 0,01. Какова при этом будет ширина доверительного интервала, если доверительная вероятность должна быть 0,997?
27. По выборке небольшого объёма сделаны оценка математического ожидания и оценка дисперсии случайной величины: 50 е.и. и 25 е.и.2, соответственно. Требуется оценить объём выборки, необходимый, чтобы относительная ошибка оценки математического ожидания не превышала 1 %.
28. Оценка математического ожидания и оценка дисперсии случайной величины составляют соответственно 141 е.и. и 64 е.и.2. Вычислить границы доверительного интервала по двукратной ошибке.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ ПО «ИНФОРМАТИКЕ И МАТЕМАТИКЕ» ПО ТЕМАМ ИЗ ТЕСТОВ МИНИСТЕРСТВА ОБРАЗОВАНИЯ






