семестр: 3
вид промежуточной аттестации: дифференцированный зачет
Вариант 9
А1. Если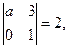 
то значение параметра а равно…
1) -5
2) 5
3) -2
4) 2
А2. Вычислить определитель третьего порядка 
5) 33
6) 30
7) 87
8) -87
А3. Установить соответствие между определителем 
и его значением
1) 5
2) 6
3) 11
4) -11
А4. Сумма x+y, где (x,y) является решением системы уравнений 
равна…
1) 1
2) -1
3) 7
4) -7
А5. Найдите координаты точки максимума функции y=g(x), заданной на интервале (-4;2)
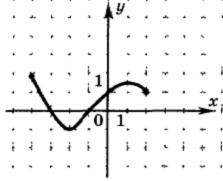
1) (-3;-1)
2) (-2;-1)
3) (1;2)
4) (-4;2)
А6. Зависимость пути от времени при прямолинейном движении точки задана уравнением 
. Вычислите ее скорость в момент времени t=3c.
1) 39 м/с
2) 22 м/с
3) 20 м/с
4) 32 м/с
А7. Найти наибольшее значение функции 
в промежутке [-2,9]
1) 3
2) 28
3) -7
4) 5
А8. Производная функции 
в точке x=0 равна…
1) 0
2) 2
3) 1
4) е
А9. Вычислите производную сложной функции 
1) 
2) 
3) 
4) 
А10. Вычислить площадь фигуры, ограниченной линиями 
1) 
кв.ед
2) 16 кв.ед
3) 2 кв.ед
4) 3 кв.ед
А11. Определенный интеграл 
равен …
1) 17
2) 15
3) 
4) 7
А12. В результате подстановки 
интеграл 
приводится к виду
1) 
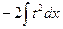
2) 
3) 
4) 
А13. Решением дифференциального уравнения 
является функция…
1) 
2) 
3) 
4) 
А14. Общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид 
, тогда корни характеристического уравнения равны
1) 
2) 
3) 
4) 
А15. Четвертый член числового ряда 
равен…
1) 48
2) 15
3) 20
4) 18
А16. Частичная сумма ряда S2 ряда 
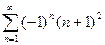равна…
1) 0
2) 1
3) 9
4) -9
А17. Пусть A={1,2,3}; B={1,3,5,6}; Найти (B 
.
1) пустое множество
2) {3}
3) {2,5,6}
4) {1,2,3,5,6}
А18. Степень вершины 10 равна…
1) 3
2) 9
3) 1
4) 2
А19. На шесть сотрудников выделены 3 одинаковые путевки в дом отдыха. Сколькими способами их можно распределить?
1) 10
2) 6
3) 3
4) 20
А20. Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов?
1) 9
2) 18
3) бесконечно много
4) 720
А21. Какова вероятность того, что наудачу выбранное целое число от 4 до 24 является кратным 6?
1) 0,5
2) 0,08
3) 0,8
4) 0,2
А22. Экзаменационный сборник по физике состоит из 80 билетов. В 50 из них встречается вопрос о лазерах. Какова вероятность, что студент Степа, выбрав билет наугад, наткнется на вопрос о лазерах.
1) 4/25
2) 0,5
3) 5/8
4) 1
А23. Закон распределения вероятностей ДСВ X имеет вид
| x | |||
| p | 0,4 | 0,3 | P3 |
тогда вероятность р3 равна…
1) 0,7
2) 0,5
3) 0,2
4) 0,3
А24. Математическое ожидание ДСВ, заданной законом распределения
| x | |||
| p | 0,2 | 0,4 | 0,4 |
равно…
1) 3,8
2) 1
3) 11
4) 3,5
Задание B.
В1. Вычислить работу, совершенную при сжатии пружины на 0,03 м, если для сжатия ее на 0,005 м нужна сила 10Н.
B2. Скорость падающего в пустоте тела определяется по формуле 
. Какой путь пройдет тело за первые 20 с падения.
В3. Найдите площадь фигуры, ограниченной линиями 
В4. Количество ребер, инцидентных вершине m
Преподаватель: __________Э.Т. Нурмухаметова
ГБОУ СПО Нефтекамский машиностроительный колледж
| Рассмотрено и одобрено на заседании ПЦК «Естественнонаучные дисциплины» Протокол №____от «__»_____2012г. |
дисциплина: Математика
Специальность: 280703 Пожарная безопасность
семестр: 3
вид промежуточной аттестации: дифференцированный зачет
Вариант 10
А1. Значение переменной x в уравнении 
равно…
1) 3
2) 0
3) 1
4) нет решения
А2. Вычислить определитель третьего порядка 
1) 10
2) 44
3) -6
4) 5
А3. Решением системы уравнений 
, решаемой методом Крамера является…
1) (2;-1)
2) (7;-2)
3) (3;2)
4) (7;2)
А4. Определитель 
равен…
1) 10
2) -29
3) 14
4) 29
А5. Функция y=f(x) определена на промежутке (-1;8). На рисунке изображен ее производной. Укажите точку минимума функции на промежутке (-1;8).
1) (3;-3)
2) (1;4)
3) (-1;1)
4) (8;2)
А6. Материальная точка движется прямолинейно по закону 
. Вычислите ее скорость в момент времени t=2c.
1) 4 м/с
2) 0 м/с
3) 8 м/с
4) 20 м/с
А7. Найти наибольшее значение функции 
в промежутке [-4,4]
1) 10
2) 0
3) -10
4) 40
А8. Производная функции 
имеет вид
1) 
2) 
3) 
4) 
А9. Дана функция 
. Вычислите значение производной в точке х=2
1) 0
2) -1
3) 3/2
4) 5
А10. Вычислить площадь фигуры, ограниченной линиями 
1) 1 кв.ед
2) 9 кв.ед
3) 12 кв.ед
4) 6 кв.ед
А11. Определенный интеграл 
равен …
1) 16
2) 10
3) 
4) 2
А12. В результате подстановки 
интеграл 
приводится к виду
1) 
2) 
3) 
4) 
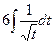
А13. Дифференциальное уравнение 
в результате разделения переменных сводится к уравнению…
1) 
2) 
3) 
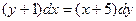
4) 
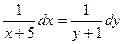
А14. Найдите общее решение дифференциального уравнения 
1) 
2) 
3) 
4) 
А15. Четвертый член числового ряда 
равен…
1) 1/7
2) -1/9
3) -1/7
4) -1/5
А16. Частичная сумма ряда S2 ряда 
равна…
1) 1/2
2) 5/6
3) 1
4) 0
А17. Пусть X={a,c}, Y={a,b,d}, Z={b,c}. Найти (X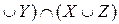 
.
1) пустое множество
2) {a,b,c}
3) {a,b}
4) {b,d}
А18. Степень вершины 1 равна…
1) 1
2) 4
3) 3
4) 2
А19. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры могут повторяться?
1) 12
2) 6
3) 11
4) 40
А20. Сколькими способами можно составить команду из 4 человек для соревнований по бегу, если в вашей группе имеются 7 бегунов?
1) бесконечно много
2) 35
3) 90
4) 10
А21. В группе 5 юношей и 20 девушек. По жребию разыгрывается один билет в театр. Какова вероятность того, что билет получит юноша.
1) 0,75
2) 0,4
3) 0,7
4) 1/5
А22. Вероятность своевременного прибытия каждого автобуса равно 0,9. Прибывают 2 автобуса. Найти вероятность того, что хотя бы один автобус прибудет вовремя.
1) 0,9
2) 1,8
3) 0,45
4) 0,81
А23. Закон распределения вероятностей ДСВ X имеет вид
| x | |||
| p | 0,1 | P2 | 0,6 |
тогда вероятность р2 равна…
1) 0,5
2) 0,3
3) 0,1
4) 0,2
А24. Математическое ожидание ДСВ, заданной законом распределения
| X | |||
| P | 0,2 | 0,3 | 0,5 |
равно…
1) 6,4
2) 45,8
3) 4,84
4) 1
Задание B.
В1. Вычислить работу, совершенную при сжатии пружины на 3 см, если для сжатия ее на 0,5 см нужна сила 10Н.
B2. Скорость падающего в пустоте тела определяется по формуле . Какой путь пройдет тело за первые 10 с падения.
В3. Вычислите площадь фигуры, ограниченной линиями 
В4. Количество ребер, инцидентных вершине 1
Преподаватель: __________Э.Т. Нурмухаметова
