(3-ий семестр, ФИМ, 2011-2012 уч.г.)
I. Кратные, криволинейные интегралы.
1. Вычислить повторный интеграл, переходя к полярным координатам:  Отв.
Отв. 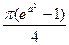
2. Вычислить площадь фигуры, ограниченной линиями:  . Отв:
. Отв: 
3. Переходя к полярным координатам, вычислить двойной интеграл  , где D – область, ограниченная окружностью
, где D – область, ограниченная окружностью  Отв:
Отв: 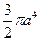
4. Изменить порядок интегрирования: 
5. Вычислить  , где D – область, ограниченная линиями x=0, x=
, где D – область, ограниченная линиями x=0, x=  , у=2. Отв:
, у=2. Отв: 
6. Найти площадь, ограниченную кривыми  Отв:
Отв: 
7. Вычислить объем тела, ограниченного поверхностями 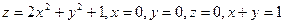 . Отв:
. Отв: 
8. Вычислить  , если тело V есть шар радиуса R.
, если тело V есть шар радиуса R.
Отв: 
9. Вычислить  , где V ограничена плоскостями х=0,у=0, z=0 и частью сферы
, где V ограничена плоскостями х=0,у=0, z=0 и частью сферы  в первом октанте.
в первом октанте.
10. Вычислить  , если тело V ограничено поверхностями
, если тело V ограничено поверхностями  Отв:
Отв:  .
.
11. Вычислить криволинейный интеграл 1-го рода:  , где
, где  . Ответ:
. Ответ:  .
.
12. Вычислить криволинейный интеграл 1-го рода: 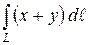 , где L – правый лепесток лемнискаты
, где L – правый лепесток лемнискаты  . Ответ:
. Ответ: 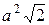 .
.
13. 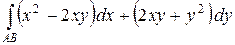 , где АВ – дуга параболы
, где АВ – дуга параболы 
от А (1, 1) до В (2, 4). Ответ:  .
.
14.Проверить, является ли заданное выражение дифференциалом некоторой функции  и в случае положительного ответа найти
и в случае положительного ответа найти  с помощью криволинейного интеграла.
с помощью криволинейного интеграла.
 ;
;
14. Вычислить:  .
.
15. Вычислить  , где С – верхняя половина эллипса
, где С – верхняя половина эллипса 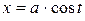 ,
,  , пробегаемая по ходу часовой стрелки.
, пробегаемая по ходу часовой стрелки.
16. Вычислить работу силового поля  вдоль первой арки циклоиды
вдоль первой арки циклоиды  .
.
- По формуле Грина вычислить криволинейный интеграл
 , взятый по замкнутому контуру
, взятый по замкнутому контуру  .
.
II. Поверхностные интегралы. Теория поля.
1.Вычислить div  (M) и
(M) и 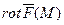 векторного поля
векторного поля  .
.
2.Вычислить grad U(M0) и  в направлении
в направлении 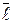 :
:
 ;
; 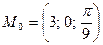
 .
.
3.Вычислить циркуляцию векторного поля  по контуру треугольника АВС, где А (1, 0, 0), В (0, 1, 0), С (0, 0, 1).
по контуру треугольника АВС, где А (1, 0, 0), В (0, 1, 0), С (0, 0, 1).
4. Найти циркуляцию векторного поля 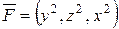 вдоль контура L – линии пересечения плоскости х + у + z = 3 c координатными плоскостями.
вдоль контура L – линии пересечения плоскости х + у + z = 3 c координатными плоскостями.
5.Вычислить поток векторного поля  (M)=(Р,Q,R) через внешнюю сторону боковой поверхности
(M)=(Р,Q,R) через внешнюю сторону боковой поверхности  , если
, если  ;
; 
6.Вычислить поток векторного поля  через полную поверхность параболоида
через полную поверхность параболоида 
7.Вычислить поток векторного поля  через поверхность пирамиды
через поверхность пирамиды 
8. Выяснить, имеет ли данное векторное поле потенциал и найти его, если он существует:  ;
;
III. Числовые и степенные ряды. Тригонометрические ряды Фурье.
1. Исследовать на сходимость, применяя признаки сходимости знакоположительных рядов.
а)  б)
б)  в)
в) 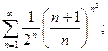 г)
г) 
д)  е)
е) 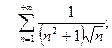
 з)
з) 
2. Исследовать на сходимость знакочередующийся ряд: а) 
б)  в)
в)  г)
г) 
3. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям (решить задачу Коши), с помощью степенного ряда:
а) 
б) 
4. Определить радиус, интервал сходимости и выяснить поведение ряда на концах интервала сходимости: а) 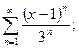 б)
б) 
5.Разложить функцию f(x) в ряд Тейлора:
а) 
б) 
6. Вычислить с точностью до 0,001: 
7. Разложить функцию f(x) в тригонометрический ряд Фурье на данном промежутке:
а)  =
=  .
.
б)  =
= 
Экзаменатор ст.преподаватель каф. ВМ Зарипова И.М.






