Типы отношений, изображаемых с помощью графа

На рис. 3.4 показаны в форме графа три типа отноше­ний (рефлексивное, симметричное и транзитивное).

Рис. 3.4. Рефлексивное (1), симметричное (2) транзи­тивное (3) отношения

Для рефлексивного отношения стрелка начинается и заканчи­вается в вершине а, поскольку отношение устанавливается между элементом и им самим. В симметричном отношении первая стрелка начинается в а и заканчивается в b, а вторая начинается в b и заканчивается в а, так как отношение устанавливается в двух направлениях. Для транзитивного отношения первая стрелка направлена от а к b, вторая - от b к с, а третья, опре­деляющая транзитивность, - от а к с.

Некоторые свойства графов

Маршруты

Маршрутом называется путь, проходящий от одной вершины к другой через ребра и вершины графа. Правильнее было бы опре­делить маршрут как последовательность ребер, образующую не­прерывный путь от исходной до конечной вершины. Если граф представляет файл или список, то последовательность ребер является поисковой последовательностью. С ее помощью можно осуществить поиск требуемой записи, анализируя записи в ячейках. Очевидно, эффективность поиска зависит от:

• структуры файла или списка его графа; • метода поиска — выбора последовательности ребер

На рис. 4.4 изображен граф с несколькими вершинами и ребрами.

Рассмотреть несколько последовательностей ребер. Самая прямая из них — acdeb. Поскольку здесь возможны ва­рианты, определим принцип их классификации. Будем считать, что последовательность ребер:

· элементарная, если в ней ни одно ребро или вершина не появляется более одного раза, например acdeb;

· простая, если в ней ни одно ребро не появляется более одного раза, например acdgjkgeb;

· непростая в остальных случаях.

Цикл

Последовательность ребер, в которой исходная и конечная вершины совпадают, называется циклом. Если последователь­ность ребер включает циклы, она не может быть элементарной. На рис, 4.5, например, последовательность gjkg является циклом, так как она берет начало и заканчивается в одной точке g.

Последовательность ребер acdgjkgeb содержит цикл gjkg. Эта последовательность является простой, так как в ней не повторя­ются ребра, но она не элементарная, так как вершина g по­является дважды.

По аналогии с последовательностью ребер можно провести классификацию циклов, разделяя их на элементарные, простые и т. д., причем к ним применимы те же определения. Воспользовавшись в качестве иллюстрации рис. 4.5, определим цикл как

· элементарный, если никакие вершины или ребра не появля­ются в нем больше одного раза, например abcda (хотя начальная и конечная вершины совпадают);

· простой, если никакое ребро не появляется более одного раза, например abcefghcda;

· непростой во всех остальных случаях, например, abcefghcba.

 

Рис 4.5 Изображение нескольких типов циклов

Маршруты орграфа

Многие структуры используют асимметричные отношения и поэтому представляются орграфами. Маршруты между различными точками орграфа называются последовательностями или цепочками дуг. Граф представляет собой удобный аппарат для передачи действий, выполняемых над такими структурами данных.

Рис 4.6 Орграф

На рис. 4.6 изображен орграф. Здесь также существует несколько последовательностей дуг между вершинами а и b. При определении таких последовательностей важно установить направление дуги. Мы можем перемещаться по дуге только в соответствии с указанием стрелки. Так, на рис. 4.6 acdgeb — элементарная последовательность дуг от а до b. Последовательность же acdeb является недопустимой, так как дуги de не существует, а есть только дуга ed.

Последовательности дуг также можно делить на: элементарные, простые и непростые, в зависимости от того, повторяется ли в них вершина или ребро.

Петли. В орграфе петли эквивалентны циклу. Петлей называется последовательность, начало и конец которой совпадают. Как и ранее мы должны помнить, что каждая дуга имеет свое направление. Петля считается определенной лишь тогда, когда из начальной точки, пройдя через различные промежуточные вершины в указанном стрелками направлении, возвратимся в исходную позицию. На рис. 4.7 показаны петли, отображающие циклы рис.4.6. Орграфы могут содержать цикл определяемые после удаления направленности из графа.

Из четырех циклов, представленных на рис. 4.7, только три являются петлями. Действительно, вершину h можно покинуть двумя путями, но нет пути, по которому можно было бы в нее вернуться.

Рис 4.7 Петли и циклы оргграфа, изображенного на рис 4.6

Петли также делятся на элементарные, простые и непростые, в зависимости от того, сколько раз встречается в них вершина или дуга.

Концепция петли, введенная теорией графов, сравнима с понятием “петли” или цикла используемым программистом. Очевидно, команды в программе можно рассматривать как вершины графа.

Дуги, которые соединяют команды, определяют последовательность, в которой ЭВМ переходит от одной команды к другой.

Геометрия

Граф представляет собой геометрическую фигуру, но принципы, которыми мы руководствуемся при его построении, отличаются от используемых в геометрии. Он не рассмат-

Рис. 4.8. Изоморфные орграфы

ривается в виде жесткой конструкции в своей плоскости. Более того, отрезки, сое­диняющие вершины, не обязательно должны быть прямыми.

На рис. 4.8 первые три орграфа графически эквива­лентны: каждый содержит три вершины и три соединяющие их, в одной и той же последовательности дуги. Их эквивалентность не зависит от того, как изображены дуги - прямыми, круговыми или волнистыми линиями. Третий и четвертый орграфы состоящие из трех дуг и трех вершин, не являются эквивалентными по теории графов. Дело в том, что в одном из них можно про­двигаться по петле в обратную сторону, а в другом нельзя.

ДЕРЕВЬЯ

Основные определения

Дерево представляет собой граф, не содержащий циклов, что упрощает его структуру.

Рис. 4.9 Дерево

Это связный граф, так как каждая вершина в нем завершает, по крайней мере, одно ребро, и не существует вершин, которые не завершали бы ребро. Вершина, у которой отсутствуют исходящие ребра, называется изолированной точкой. Изолированная точка в дерево входить не может. Более того, дерево с v вершинами обязательно включает v - 1 ребер. Пример дерева показан на рис.4.9

Генерация

Причину наличия в дереве v — 1 ребер можно выяснить, рассмотрев процесс его генерации. Начнем с простого дерева - единственной вершины. Добавляя к нему вершины, можно генерировать более сложные деревья. Всякий раз мы соединяем новую вершину при помощи ребра с какой-либо другой, введенной ранее. Таким образом, на втором этапе у нас уже будет две вершины и соединяющее их ребро.

Предположим, мы сгенерировали дерево, изображенное на рис.4.10 Добавим к нему вершину h. Она является изолированной точкой

 

Рис. 4.10. Генерация дерева

Чтобы эта точка стала частью дерева, добавим ребро, соединяющее h с некоторой вершиной (на рисунке hf). Если попытаться ввести дополнительное ребро, соединяющее h с какой-либо другой вершиной, то образуется цикл. Другими словами, если вслед за hf мы добавим ребро hg, то получим цикл hfgh, и граф на рис. 4.10 перестанет быть деревом.

Типы вершин

Число ребер, которые оканчиваются одной вершиной, называется инциденцией. В зависимости от инциденции для дерева определяются два типа вершин;

• висячая, которая инцидентна только к одному ребру;

• точка ветвления, или узел, инцидентный по крайней мере к двум ребрам.

На рис. 4.10 a, b, e, g - висячие вершины, с, d и f - узлы. Очевидно, их можно рассматривать как часть последовательности ребер, соединяющих другие вершины.

Деревья-орграфы

Вернемся к рассмотренной выше структуре и заменим в ней ребра дугами. В результате получим орграф, который также является деревом, - дерево-орграф. Эта структура вызывает больший интерес, чем дерево, так как является средством представления иерархической организации.

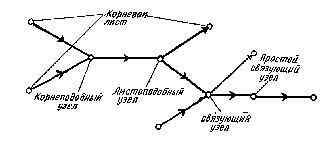Рис..4.11. Направленное дерево

В зависимости от направления дуги здесь различают два типа висячих вершин:

• корень, который имеет одну или несколько исходящих дуг и ни одной входящей;

лист, который имеет одну или несколько входящих дуг и ни одной исходящей.

Тип узла также определяется направлением связанной с ним дуги и, кроме того, инциденцией. Выделяются следующие типы узлов:

• корнеподобный, имеющий больше входящих дуг, чем исхо­дящих;

• листоподобный, имеющий больше входящих дуг, чем исхо­дящих;

• связующий, в котором число входящих дуг равно числу

исходящих;

• простой связующий с одной входящей и одной исходящей дугами (инцнденция равна двум).

Корни, листья и все типы узлов изображены на рис.4.11.

Древовидная структура

Направленное дерево - это простая структура орграфа. Еще более простой древовидной структурой является направленное дерево с одним корнем (иногда его называют древовидной структурой с корнем).

Корень рассматривается как источник направленной древовидной структуры. От корня до любого листа легко проследить элементарную последовательность дуг. Число дуг между корнем и листом называется уровнем листа. Аналогично число дуг между корнем и узлом определяет уровень узла.

Рис. 4.11. Древовидная структура

Практическая ценность древовидной структуры не вызывает сомнений. Примером такого графа может служить схема управления какой-либо организации. Корнем здесь является президент или директор. От корня исходят одна или несколько дуг к заместителям, которые занимают первый уровень. По мере удаления от корня располагаются' более низкие уровни управления. Наконец, в качестве листьев выступают рабочие, которые и завершают эту схему. Древовидная структура показана на рис.4.11.

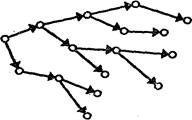
Двоичное ветвление. Древовидная структура с двоичным ветвлением содержит всего четыре типа вершин:

• один корень — источник этой древовидной структуры;
• листья— направления роста дерева;
• простые узлы, связывающие предшествующий уровень со следующим за ним (они могут появиться на любом уровне);
• простые корнеподобные узлы. с одной входящей и двумя исходящими дугами (инциденция равна трем), составляющие единственно возможный другой тип узла.

Древовидная структура с двоичным ветвлением представляет простую программу, не содержащую петель, в которой условные переходы могут определять только одно направление. Одна из таких структур изображена на рис.4.12.

Транзитивные графы

Более простым типом графа является транзитивный граф — связный орграф, в котором могут присутствовать циклы и не мо­гут - петли. Это обеспечивает сохранение транзитивности. На рис. 4.13 изображен транзитивный орграф с корнем.