ТЕКСТЫ С ФОРМУЛАМИ 13
Фрагмент 1. Позиционные системы счисления
В позиционной системе счисления количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра этого числа. Например, меняя позицию цифры 7 в десятичной системе счисления, можно записать разные по величине десятичные числа, например, 7; 70; 7000; 0,07 и т.д.
В общем случае любое число N в позиционной системе счисления можно представить в виде:
N=ak-1*pk-1+…+a1*p1+a0*p0+a-1*p-1+…+a-n*p-n
где 
- (k –1)-ая цифра целой части числа N, записанного в системе счисления с основанием p;
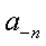- n-ая цифра дробной части числа N, записанного в системе счисления с основанием p;
k - количество разрядов в целой части числа N;
n - количество разрядов в дробной части числа N;
Максимальное число, которое может быть представлено в к разрядах
.
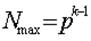Минимальное число, которое может быть представлено в n разрядах
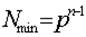
Имея в целой части числа к разрядов, а в дробной n разрядов, можно записать всего 
разных чисел.
С учетом этих обозначений запись числа N в любой позиционной системе счисления с основанием p имеет вид:
Фрагмент2. Формы представления чисел в компьютере
В компьютерах применяются две формы представления двоичных чисел:
- естественная форма или форма с фиксированной запятой (точкой);
- нормальная форма или форма с плавающей запятой (точкой).
В естественной форме (с фиксированной запятой) все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
Если используется система счисления с основанием p при наличии k разрядов в целой части и n разрядов в дробной части числа, то диапазон значащих чисел N при их представлении в форме с фиксированной запятой, определяется соотношением:
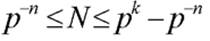
Например, при p =2, k =10, n =6 диапазон значащих чисел будет определяться следующим соотношением:
В нормальной форме (с плавающей запятой) каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок – целым числом. В общем виде число в форме с плавающей запятой может быть представлено в виде:
,
где M – мантисса числа (| M | < 1);
r – порядок числа (r - целое число);
p – основание системы счисления.
Фрагмент 3. Моделирование жизненного цикла продукта
Модель описывает процесс распространения продукта. Изначально продукт никому не известен, и для того, чтобы люди начали его приобретать, он рекламируется. Влияние рекламы можно оценить ее эффективностью, т.е. степенью воздействия на людей. В итоге определенная доля людей приобретает продукт. На дальнейшее распространение продукта начинает влиять не только реклама, но и фактор общения между собой владельцев продукта и потенциальных потребителей. Этот фактор зависит от силы убеждения владельца. Процесс приобретения товара можно рассматривать как поток – «перетекание» потенциальных покупателей в «стан» владельцев. Этот поток тем сильнее, чем больше людей охвачено рекламой и чем больше людей общается с владельцами товара. Естественно, что чем больше людей уже купили товар, тем слабее становится поток, и в конце концов он «иссякает», т.е. приобретение товара заканчивается.
Математическая модель процесса описывается следующей системой алгебро-дифференциальных уравнений:
Здесь:
А - численность населения;
B - эффективность рекламы;
C – частота контактов;
F - сила убеждения;
х - потенциальные покупатели;
y – потребители;
z - интенсивность приобретения продукта;
r - интенсивность приобретения под влиянием рекламы;
s - интенсивность приобретения под влиянием общения.
