Задание: графически и численно решить систему нелинейных алгебраических уравнений, на примере поиска точек пересечения двух функций.
Исходные данные:
график строится по исходным данным, определяемым в виде констант в программе:
а) координаты верхнего левого угла прямоугольника, в котором должен быть расположен график;
б) размеры прямоугольника;
в) количество линий координатной сетки по каждой из осей;
г) диапазон изменения аргумента;
Решение нелинейного алгебраического уравнения проводить одним из методов:
- простых итераций;
- дихотомии (деления отрезка пополам);
- пошаговых приближений.
Примерный внешний вид результата решения на экране:
 Как видно из этого рисунка на экране должны быть изображены:
Как видно из этого рисунка на экране должны быть изображены:
- графики функций,
- оси координат,
- координатная сетка,
- предельные значения по осям.
А также должны присутствовать координаты точек пересечения, например:
X -0.8 +0.8
Y +0.7 +0.7
Также должно быть предусмотрено сохранение:
1) координат точек пересечения в типизированном файле;
2) таблицы обеих функций в отдельных нетипизированных файлах (под таблицей функции подразумевается двумерный массив, первый столбец которого – это значения аргумента, а второй – значения функции).
Варианты заданий
| Таблица № 1 | ||
| № | система уравнений | отрезок аргумента |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<3 | |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<5 | |

| -5<x<5 | |
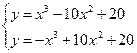
| -5<x<10 | |

| -5<x<10 | |

| -5<x<5 | |

| 0.5<x<1 | |

| 0.5<x<1 |
Напомним, что решение нелинейного алгебраического уравнения вида F(x) = 0 состоит в том, чтобы найти такие значения переменной x, при которых значение функции F(x) обращается в нуль. Поиск решения уравнения ведется в пределах отрезка значений аргумента x. Отрезок, на котором ведется поиск решения, в данной задаче задан. Процесс поиска итерационный. Общий алгоритм поиска для всех трех методов решения следующий:
1. Задается начальное значение для аргумента x
2. По значению аргумента x вычисляется новое значение аргумента x.
3. Проверяется условие достижения наперед заданной точности и, если условие выполняется, то вычисленное значение принимается за решение, в противном случае алгоритм повторяется, начиная со 2-го пункта.
Для обеспечения сходимости итерационного процесса в зависимости от алгоритма метода должно быть выполнено несколько условий.
Для использования метода простых итераций необходимо выполнение следующих условий:
1. Решение уравнения в пределах указанного отрезка должно быть единственным.
2. Уравнение F(x) = 0 можно преобразовать к виду x = f(x).
3. Первая производная функции f(x) должна быть меньше 1 на всем отрезке.
В данном методе на каждом шаге итерации вычисляется очередное значение x, по формуле x = f(x). Вычисления заканчиваются, когда разность предыдущего и нового значений x станет меньше заданной точности вычисления корня.
// функция f(x)
function f (x: real): real;
begin
f:= sin (x) + 0.25;
end;
var x, e: real;
begin
writeln ('Решение уравнения x = sin(x) + 0.25 методом простых итераций');
writeln;
write ('Задайте начальное значение x x0 = ');
readln (x);
write ('Задайте погрешность вычисления результата e = ');
readln (e);
while abs (f (x) - x) >= e do
begin
x:= f (x);
writeln (x: 12: 9);
end;
writeln;
writeln('Корень уравнения x = ', x: 12: 9);
write('Для продолжения нажмите <Enter>');
readln;
end.
Метод деления отрезка пополам (дихотомии) можно применять, при условии, что на выбранном отрезке есть только один корень, и реализуется следующим алгоритмом:
1. Исходный отрезок [a,b], на котором ищется корень, делится пополам.
2. Если значение функции F(x) в середине отрезка совпадает по знаку с левой границей отрезка, то левая граница отрезка переносится в середину отрезка, в противном случае в середину отрезка переносится правая граница.
3. Если размеры отрезка больше заданной точности, то повторить действия, начиная с первого пункта, в противном случае любая из границ отрезка принимается за решение.
function F (x: real): real;
begin
F:= x - sin (x) - 0.25;
end;
var
a, b, x, e: real;
begin
writeln;
writeln('Решение уравнения x-sin(x)-0.25=0 методом дихотомии');
writeln;
repeat
writeln('Задайте границы отрезка [a,b], причем а<b ');
write('a = ');
readln (a);
write('b = ');
readln (b);
until b > a;
write('Задайте погрешность вычисления результата e = ');
readln (e);
repeat
x:= (a + b) / 2;
if F (x) * F (a) > 0
then a:= x
else b:= x;
until (b - a) < e;
writeln('Корень уравнения x = ', x: 12: 9);
write('Для продолжения нажмите <Enter>');
readln;
end.
Метод пошаговых приближений позволяет найти все решения на заданном отрезке и реализуется следующим алгоритмом:
1. По виду графика выбирается начальное значение шага таким, чтобы оно было меньше расстояния между ближайшими корнями.
2. На каждом шаге по значениям функций в граничных точках проверяется наличие корня на выбранном отрезке.
3. Если корень есть, то величину шага уменьшают в заданное число раз, например, N=5.
4. Если значение полученного шага меньше, чем заданная точность, деленная на N, то начало отрезка принимается за корень. иначе выполняют действия, начиная с пункта 2.
Для определения отрезка, на котором есть корень в приведенном ниже примере используется функция SubRange, а для вычисления корня - функция Root.






