Цель работы
Изучить уравнения и законы поступательного и враща-
тельного движения тел.
Определить экспериментально кинематические и дина-
мические характеристики движущихся тел.
Описание установки
Экспериментальная ус-
тановка состоит из стойки с
укреплённым на ней с по-
мощью подшипника шки-
вом и столика, жёстко свя-
занного со шкивом. Шкив и
столик имеют общую ось
вращения. На
шкив наматывается нить.
Ко второму концу нити,
перекинутой через блок,
подвешивается груз массой
m. Опускаясь с высоты h,
груз приводит во враща-
тельное движение шкив со
столиком. В работе изуча-
ется движение системы связанных тел – груза и шкива со столиком.
3.Формулы для расчета
Уравнение для координаты при равноускоренном движении
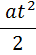
где a – ускорение груза; t – время его движения с высоты h до
пола.
Расчётные формулы для конечной скорости груза
u= 
и его ускорения
a= 
Расчётные формулы для кинематических характеристик
вращательного движения столика со шкивом:
= 
= 
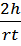ε= 
= 
φ 
или φ= 
где – угловая скорость столика в конце его ускоренного вра-
щения; ε – угловое ускорение столика; φ – угол поворота радиу-
са r шкива за время движения груза.
За это время столик сделает N оборотов:
N = 
Сила натяжения нити
F н = m (g - a).
В конце движения груз имеет скорость u, импульс P = m u;
кинетическую энергию
E кгр= m u2/2; начальная потенциальная
энергия груза E п = mgh.
Динамическое уравнение вращательного движения столика
имеет вид
Mн+Mтр=Jἑ
где M н= [ rF н ] – момент силы натяжения нити; J – момент инер-
ции шкива со столиком; ε– их угловое ускорение.
В проекции на ось вращения ОО уравнение записыва-
ется в виде
М н - М тр = Jε
откуда момент инерции J столика со шкивом равен
Момент силы натяжения нити равен
M н = mr (g - a)
где m – масса груза; а – его ускорение; r – радиус шкива.
Момент силы трения M тр можно определить эксперимен-
тально подбором минимальной массы груза m 0, при которой его
движение будет равномерным (а= 0). Уравнение движения
груза для этого случая имеет вид
FНО = m 0 g.
Момент этой силы равен
M тр = MНО = m 0 gr.
Кинетическая энергия в конце ускоренного движения равна
Ekст= 
Работа момента сил трения за время ускоренного вращения
столика будет определяться
A тр = M трφ
| № П/п | t, c | <t>, c | u, м/c | a, м/c2 | ω, c-1 | Ε, c-2 | φ, рад | N, Об. | ||||||||
| r= м | M= кг | H= м | ||||||||||||||
Кинематические характеристики движения груза и шкива со столиком (таблица 1)
Кинематические характеристики движения груза
и шкива со столиком и телом (таблица 2)
| № П/п | t, c | <t>, c | u, м/c | a, м/c2 | ω, c-1 | Ε, c-2 | φ, рад | N, Об. | ||||||||
. По формуле рассчитайте момент силы трения
M тр для каждого опыта;
. По формуле рассчитайте момент инерции столи-
ка со шкивом J 1 (значение углового ускорения ε1 возьмите из
табл.1) и системы столик со шкивом – тело J 2. Момент инерции
тела J тела находится как разность J 2 и J 1:
J тела = J 2 - J 1.
Рассчитайте теоретическое значение момента инерции тела:
- для стержня Jтеор= 
где m ст – масса стержня; l – его длина;
- для диска Jтеор= 
где m д – масса диска; R – его радиус.
Результаты расчёт динамических характеристик
поступательного движения груза (таблица 3)
| Условия опытов | a | Fн | u | P | Eк гр | Eп |
| м/с2 | Н | м/c | Кг м/c | Дж | Дж | |
| Без тела на столе | ||||||
| С телом на столе |
Расчёт динамических характеристик
вращательного движения столика (таблица 4)
| Характеристики Условия Опытов | Мн | m0 | Mтр | J1 | J2 | Jтеор | Eкст | Атр | L |
| Н м | кг | Нм | Кгм2 | Кгм2 | Кгм2 | Дж | Дж | 
| |
| Без тела на столиике | |||||||||
| С телом на столике |
Вывод:
