ПЕРВИЧНАЯ ОБРАБОТКА ВЫБОРКИ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
Под генеральной совокупностью с функцией распределения Fξ(x) будем понимать гипотетическую совокупность всех возможных значений случайной величины ξ. Вместо функции распределения Fξ(x) может использоваться плотность распределения fξ(x), либо закон распределения ξ, заданный в виде таблицы.
Набор n значений случайной величины, полученных в результате эксперимента, называется выборкой объема n из генеральной совокупности, а числа х1, х2,..., хn – выборочными значениями случайной величины ξ.
Выборке { х1, х2,..., хn } поставим в соответствие случайную величину, принимающую эти значения с вероятностями 1/n:
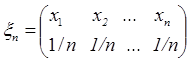
и будем называть ее выборочным распределением.
Первичная обработка выборки включает следующие операции:
1) упорядочение по возрастанию х1 < х2 <... < хn, приводит исходные данные к выборке, которая называется вариационным рядом;
2) вычисление частоты ni элемента zi в том случае, когда z1, …, zk представляют разные (не равные между собой) числа в исходной выборке { х1, х2,..., хn } так, что ni равно числу повторяющихся элементов, соответствующих zi (i = 1, …, k); полученная таким образом новая выборка { zi, ni } называется статистическим рядом;
3) вычисление относительной частоты νi = ni/n и последовательных сумм ν1+ ν2 + …+ νi, которые представляют накопленные частоты элемента zi.
Для получения статистического ряда { zi, ni } может использоваться и более общий механизм, когда zi представляет не просто равные элементы, а близкие в определенном смысле. Например, это могут быть элементы, попадающие в i -й полуинтервал вида [ xi, xi+1).
Если функция распределения зависит то некоторого параметра θ, то есть Fξ(x) = Fξ(x, θ), то можно рассмотреть задачу оценивания этого параметра по n значениям выборочных данных { х1, х2,..., хn }. Функцию θn от этих значений будем называть оценкой параметра θ.
Если в качестве оценок используются выборочные характеристики случайной величины, оценки называются точечными. Такими оценками являются:
§ выборочное среднее
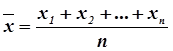 ,
,
для нахождения которого в Excel используется функция СРЗНАЧ (x1;x2;…,xn);
§ выборочная дисперсия
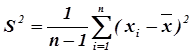
для нахождения которой в Excel используется функция ДИСП (x1; x2; …, xn).
Если для параметра θ можно указать некоторый интервал (θ1, θ2), для которого
p (θ1 < θ < θ2) = 1 – α,
где α – малое число, называемое уровнем значимости, то говорят об интервальных оценках. Интервал (θ1, θ2) называется доверительным интервалом для параметра θ с доверительной вероятностью 1 – α. В рассматриваемых упражнениях будем строить симметричные интервалы вида (θ1, θ2) = (θn - Δ, θn + Δ) для точечной оценки θn параметра θ.
При известной дисперсии σ2 нормальной генеральной совокупности значение Δ для математического ожидания задается формулой
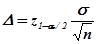 ,
,
где z1-α/2 вычисляется c помощью функции Excel НОРМСТОБР(вероятность).
Пример 1
В ходе исследования рецидивной преступности из документов были собраны данные о числе повторных судимостей двадцати случайно отобранных человек, имевших в прошлом одну или более судимостей. Число повторных судимостей приведено в таблице:
Задача:
· Провести первичную обработку рассматриваемых данных, построить график накопленных относительных частот и найти доверительный интервал с уровнем значимости α = 0,05






