Основные формы статистического распределения
Кривая распределения выражает закономерность распределения единиц совокупности по величине варьирующего признака и представляет собой графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант (гистограмма, полигон). Различают эмпирические и теоретические кривые распределения:
Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.
Теоретическая кривая распределения – это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения.Различают следующие виды эмпирических кривых распределения:
1.одновершинные кривые, которые, как правило, характерны для однородных совокупностей:
• симметричные;
• несимметричные: умеренно-ассиметричные, крайне – ассиметричные; V-образные.
2. многовершинные кривые – характеризуют неоднородные совокупности распределения явлений, появление двух и более вершин приводит к необходимости перегруппировки данных с целью выявления более однородных групп.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой.
Несимметричное распределение:
Умеренно-ассиметричное распределение – такой вид распределения, при котором малая часть частот находятся по одну сторону от центра распределения, а большая часть частот находится по другую сторону на одинаковом расстоянии. Нормальное распределение, также известное, как распределение Гаусса, является одним из наиболее известных непрерывных распределений.
В качестве некого стандарта теоретического закона распределения выступает нормальный закон распределения, с которыми сравниваются другие распределения.
Распределение признаков совокупности называется нормальным, если этот признак представляет собой результат воздействия множества факторов случайных и независимых или слабозависимых, и влияние каждого из них мало по сравнению с общим воздействием факторов.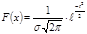 
Величина нормированного отклонения вычисляется в этом случае по 
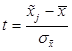формуле:
Понятия о моментах статистического распределения
Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения, предложенные
русским математиком П.Л. Чебышевым и успешно примененные А.А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм большого, но конечного числа независимых случайных величин.
Моментом распределения называется средняя арифметическая величина тех или иных степеней отклонений индивидуальных значений признака от определенной исходной величины.
Моментом k-го (Мk) порядка называют среднюю отклонений вариантов от некоторой постоянной величины А в степени k:
, 
,
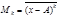
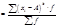где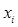 
– значения признака;
А – постоянная величина, от которой определяются отклонения;
k – степень отклонения (порядок момента).
При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности. При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей – теоретическими.
