Оцінювання інтенсивності структурних зрушень: лінійний та квадратичний коефіцієнти структурних зрушень.
Узагальнюючими показниками структурних зрушень у випадках, коли виникає необхідність оцінити структурні зрушення у соціально-економічному явищі в цілому за якісь окремі часові періоди або у кількох структур, що відносяться до окремих об’єктів за один і той же часовий період, є лінійний та квадратичний коефіцієнти “абсолютних” структурних зрушень, які визначають за формулами:
Лінійний коефіцієнт “абсолютних” структурних зрушень
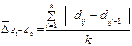 , (4.7.3)
, (4.7.3)
де k – кількість структурних частин сукупності;
dij - питома вага (частка) і - ої частини сукупності в j – ий період часу;
dij- 1- питома вага (частка) і - ої частини сукупності в (j – 1) період часу.
Квадратичний коефіцієнт “абсолютних” структурних зрушень
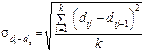 . (4.7.4)
. (4.7.4)
Лінійний та квадратичний коефіцієнти “абсолютних” структурних зрушень (у процентних пунктах) дозволяють отримати зведену оцінку швидкості зміни питомої ваги окремих частин сукупності. Для зведеної характеристики інтенсивності зміни питомої ваги окремих частин сукупності використовують квадратичний коефіцієнт відносних структурних зрушень:
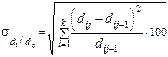 , (4.7.5)
, (4.7.5)
Цей показник відображає той середній відносний приріст питомої ваги (у відсотках), який спостерігався за період, що досліджується.
Для зведеної оцінки структурних зрушень у досліджуваній сукупності в цілому за весь часовий інтервал, що охоплює кілька тижнів, місяців, кварталів чи років, найбільш доцільно використовувати лінійний коефіцієнт “абсолютних” структурних зрушень за n періодів (у процентних пунктах) :
 , (4.7.6)
, (4.7.6)
де din - питома вага (частка) і - ої частини сукупності в останній період часу;
di 1- питома вага (частка) і - ої частини сукупності в 1 - ий період часу.
Цей показник може використовуватися як для порівняння динаміки двох і більше структур, так і для аналізу динаміки однієї і тієї ж структури за різні за тривалістю періоди часу.
Поняття, складові елементи та об’єктивні умови для побудови рядів динаміки (часових рядів), їх види та особливості.
Однією з особливостей суспільних явищ є їх безперервний розвиток у динаміці. Так, протягом певного часу (за годину, день, місяць, рік) мають місце відповідні зміни соціально-економічних явищ: кількість населення; споживання електроенергії; продуктивність праці; урожайність зернових культур тощо. Тому одним із важливих завдань статистики є вивчення суспільних явищ у їх розвитку за часом. Це завдання вирішують побудовою та аналізом рядів динаміки.
Рядом динаміки, або динамічним рядом, називають ряд розміщених у хронологічній послідовності числових даних (статистичних показників), які характеризують величину суспільного явища на даний момент або за певний період часу.
Ряди динаміки складаються з двох елементів: рівнів ряду у і. (і=1...n) та часу ti. Рівнями ряду називають числові дані того чи іншого показника ряду динаміки; вони можуть бути виражені в абсолютних, відносних та середніх величинах і задаватися в табличній формі або графічно. Час ряду відповідає конкретним моментам або періодам, до яких відносяться рівні.
Моментними називають такі ряди динаміки, рівні яких фіксують стан явища на даний момент часу (дату). Прикладом моментного ряду динаміки можуть бути дані про чисельність населення України на початок року (млн. осіб):
Таблиця 6.1
| Рік | |||
| Чисельність населення | 51,7 | 48,5 | 47,6 |
Рівні моментного ряду підсумуванню не підлягають, так як мають елементи повторного рахунку (окремі особи, які приймали участь в перепису населення в 2002 році, приймали участь в перепису і в 2004 році). В той же час певний сенс має розрахунок різниць рівнів моментного ряду, так як вони характеризують зміну рівнів за певний проміжок часу: за період з 1989 по 2002 роки чисельність населення зменшилась на 3,2 млн. осіб, а між переписами 2002 та 2004 роками - на 0,9 млн. осіб.
Інтервальним називають такий ряд, рівні якого характеризують явище за певний період часу. Прикладом інтервального ряду динаміки є виробництво промислової продукції регіону за 2000-2003 pp. (млн.грн):
Таблиця 6.2
| Рік | ||||
| Виробництво промислової продукції, млн. грн |
Рівні інтервальних рядів дають підсумкові, результативні показники, які відповідають інтервалу часу, тому їх можна підсумовувати та ділити. При складанні рівнів ряду знаходять накопичені підсумки.






