Метод деления отрезка пополам заключается в следующем. Проверяется наличие корня на отрезке [a, b] (рис.4.4).
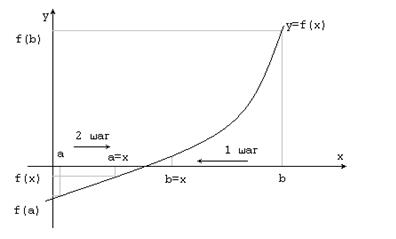
Рис.4.4. Метод деления отрезка пополам.
Для этого вычисляются значения функций f(a) и f(b). Если f(a)*f(b)>0, то уравнение не имеет корней на заданном отрезке. Если f(a)*f(b)<0, т.е. на концах отрезка [a, b] функция f(x) имеет противоположные знаки, то искомый корень лежит на этом отрезке. Поиск корня происходит следующим образом. Находим в точке a значение функции y1 = f(a). Затем определяем значение x как среднюю точку между а и b, вычисляем значения y2 = f(x). Теперь, если f(a)*f(x)>0, то корень находится на отрезке [x, b], иначе – на отрезке [a, x]. В соответствии с этим, перемещаем точку а вправо или точку в влево, выполняя, соответственно присваивание а = х или b = x. Таким образом, получаем второй отрезок [a, b], но вдвое меньший предыдущего. Процесс деления отрезка пополам продолжаем до тех пор, пока отрезок [a, b] не станет меньше заданной точности. После этого вычисляем значение x = (a+b)/2.
Пример 4.4. Решение уравнения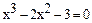 
с заданной точностью e = 0.01 методом деления отрезка пополам, если корень находится на отрезке [1,3].
#include <iostream>
#include <conio.h>
#include <math.h>
#include <stdlib.h>
using namespace std;
int main()
{ int n = 0;
float x, a = 1, b = 3, y1, y2, eps = 0.001, e, r, l;
l = a; r = b;
y1 = a*a*a – 2*a*a – 3;
y2 = b*b*b – 2*b*b – 3;
if (y1*y2>0) { cout << "Корней нет" <<endl;
getch();
exit(1);
}
do { ++n;
x = (a+b)/2;
y1 = a*a*a – 2*a*a – 3;
y2 = x*x*x – 2*x*x – 3;
if (y1*y2>0) a = x;
else b = x;
} while ((b – a)>eps);
x = (a + b)/2;
cout << "Корень уравнения на отрезке "<< l << ", " << r << "равен " << x << " и получен за " << n <<"шагов";
cout << endl;
return 0; }
Контрольные вопросы
Варианты заданий
Задание 1
Ввести с клавиатуры х и точность вычисления Eps. Вычислить с заданной точностью сумму
| Номер варианта | Задание |
| 1, 16 |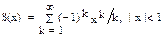 
|
| 2, 17 |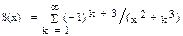 
|
| 3, 18 |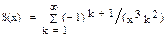 
|
| 4, 19 | 
|
| 5, 20 |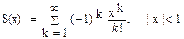 
|
| 6, 21 | 
|
| 7, 22 |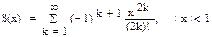 
|
| 8, 23 |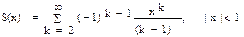 
|
| 9, 24 | 
|
| 10, 25 | 
|
| 11, 26 |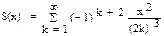 
|
| 12, 27 |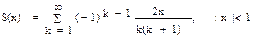 
|
| 13, 28 |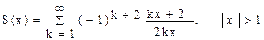 
|
| 14, 29 | 
|
| 15, 30 | 
|
Задание 2
| Номер варианта | Задание |
| 1, 16 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения x + ln(x + 0.5) – 0.5 = 0 на интервале [0, 2]. Абсолютная погрешность не превышает 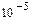 . Сравнить методы вычисления.
|
| 2, 17 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения 2x3 + 4x – 1 = 0 на интервале [0, 0.5]. Абсолютная погрешность не превышает 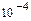 . Сравнить методы вычисления.
|
| 3, 18 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения 1/x = sin x на интервале [0.1, 2]. Абсолютная погрешность не превышает 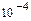. Сравнить методы вычисления.
|
| 4, 19 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 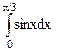 . Точность не превышает 0.001. Сравнить методы вычисления.
|
| 5, 20 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения x4 + 2x3 – x – 1 = 0 на интервале [0, 1]. Абсолютная погрешность не превышает 0.00015. Сравнить методы вычисления. |
| 6, 21 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения x3 + 12x – 2 = 0 на интервале [0.1, 1]. Абсолютная погрешность не превышает 0.00015. Сравнить методы вычисления. |
| 7, 22 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 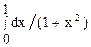 . Точность не превышает 0.001. Сравнить методы вычисления.
|
| 8, 23 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения x5 – x – 0.2 = 0 на интервале [0.9,1.1]. Абсолютная погрешность не превышает 0.0001. Сравнить методы вычисления. |
| 9, 24 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения 5x + 8lnx – 1 = 0 на интервале [0.5, 1]. Абсолютная погрешность не превышает 0.0015. Сравнить методы вычисления. |
| Номер варианта | Задание |
| 10, 25 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 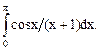 Точность не превышает 0.001. Сравнить методы вычисления.
|
| 11, 26 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравненияx3 – 2x2 + x – 3 = 0на интервале [2.1, 2.2]. Абсолютная погрешность не превышает 0.001. Сравнить методы вычисления. |
| 12, 27 | Методом деления отрезка пополам и методом итераций найти приближенное значение корня уравнения x3 + x2 – 3 = 0 на интервале [0.5, 3]. Абсолютная погрешность не превышает 0.00001. Сравнить методы вычисления. |
| 13, 28 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 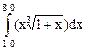 . Точность не превышает 0.001. Сравнить методы вычисления.
|
| 14, 29 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 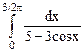 . Точность не превышает 0.001. Сравнить методы вычисления.
|
| 15, 30 | По формуле Симпсона и методом прямоугольников вычислить приближенное значение интеграла 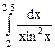 . Точность не превышает 0.001. Сравнить методы вычисления.
|
