3. В цехе 5 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найдите вероятность того, что в данный момент включено не менее 2 моторов.
4. Устройство состоит из 400 элементов, работающих независимо один от другого. Вероятность отказа любого элемента, проработавшего время t, равна 0,15. Найдите наивероятнейшее количество приборов, которые могут отказать через время t и вероятность отказа такого количества.
5. При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется от 700 до 820 годных.
6. В ящике 100 шаров, из них 20 синих, 30 черных и 50 красных. Шар вынимают наугад, фиксируют его цвет и возвращают его в ящик. Проводится 6 таких испытаний. Х – число вынутых черных шаров в этих испытаниях. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения 
и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения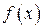 
.
Вариант 12
1. В трех урнах имеются белые и черные шары. В первой урне – 3 белых и 1 черный шар, во второй урне – 6 белых и 4 черных шара, в третьей урне – 9 белых и 1 черный шар. Из наугад выбранной урны случайным образом вынимается шар. Найдите вероятность того, что он белый. Если извлечен белый шар, то из какой урны вероятнее всего он извлечен?
2. Прядильщица обслуживает 1 000 веретен. Вероятность обрыва нити на 1 веретене в течение 1 мин равна 0,003. Вычислите вероятность того, что в течение 1 мин произойдет не более двух обрывов.
3. Вероятность изготовления стандартной детали на автоматическом станке равна 0,9. Найдите вероятность того, что из 8 взятых наудачу деталей не менее 7 окажутся стандартными.
4. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,2. Найдите вероятность того, что в 150 испытаниях событие наступит 5 раз.
5. Было посажено 400 деревьев. Вероятность того, что отдельное дерево приживется, равна 0,8. Найдите вероятность того, что число прижившихся деревьев больше 300.
6. В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. Х – число извлеченных бракованных деталей. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .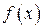
Вариант 13
1. Сборщик получил 3 коробки деталей, изготовленных заводом № 1 и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна равна 0,9, а завода № 2 – 0,8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найдите вероятность того, что извлечена стандартная деталь. Если извлечена стандартная деталь, то какова вероятность того, что она изготовлена: а) заводом № 1; б) заводом № 2?
2. В зрительном зале находится 400 человек. Какова вероятность того, что среди них имеется 3 левши, если левши в среднем составляют 1%?
3. Рабочий обслуживает три станка. Вероятность того, что в течение смены станок потребует его внимания, равна 0,7. Найдите вероятность того, что в течение смены внимания рабочего потребуют два станка.
4. Фабрика выпускает 75% продукции первого сорта. Чему равна вероятность того, что из 300 изделий число первосортных изделий равно 220?
5. Средний процент нарушений работы кинескопа телевизора в течение гарантийного срока равен 22. Вычислите вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок.
6. При бросании двух игральных костей игрок выигрывает 25 руб., если на обеих костях выпадает по 6 очков; 3 руб. – если на одной кости выпало 6 очков; 1 руб. – если сумма выпавших очков равна 6. Х – размер выигрыша, возможный при одном бросании. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
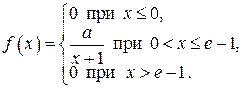
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .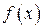
Вариант 14
1. В каждой из урн содержится 2 черных и 8 белых шаров. Из первой урны наудачу извлечен 1 шар и переложен во вторую урну, после чего из второй урны извлечен шар. Найдите вероятность того, что шар, извлеченный из второй урны, окажется белым. Если извлеченный шар оказался белым, то какова вероятность того, что из первой урны извлечен и переложен во вторую урну: а) белый шар; б) черный шар?
2. Завод отправил партию консервов в 2 000 штук. Вероятность того, что консервная банка будет разгерметизирована, равна 0,0035. Какова вероятность того, что разгерметизировано будет не более 5 банок консервов?
3. Вероятность попадания в цель составляет при отдельном выстреле 0,8. Найдите вероятность от 2 до 4 попаданий при 6 выстрелах.
4. Вероятность изготовления детали с номинальными размерами равна 0,7. Вычислите вероятность того, что среди 300 деталей номинальными будут 200 деталей.
5. При автоматической прессовке карболитовых болванок 2/3 общего числа из них не имеют зазубрин. Найдите вероятность того, что из 450 взятых наудачу болванок, количество болванок без зазубрин заключено между 280 и 320.
6. В первой урне содержится 3 белых и 5 черных шаров, во второй урне – 6 белых и 4 черных шара, в третьей урне – 1 белый и 3 черных шара. Из каждой урны вынимают по 1 шару. Х – число извлеченных черных шаров. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
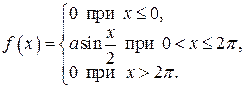
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .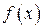
Вариант 15
1. На трех станках в одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30%, на третьем – 60% всех деталей. Вероятность каждой детали быть качественной равна 0,7, если она изготовлена на первом станке, 0,8 – если она изготовлена на втором станке, 0,9 – если она изготовлена на 3 станке. Найдите вероятность того, что наугад взятая деталь окажется качественной. Если случайно взятая деталь оказалась качественной, то какова вероятность того, что она изготовлена на третьем станке?
2. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе из 3 000 орудий.
3. Рабочий обслуживает 4 станка. Каждый станок в течение 8 часов работы простаивает из-за поломки 0,8 часа, причем остановки в любой момент времени равновероятны. Определите вероятность того, что в данный момент времени простаивают менее 2 станков.
4. Вероятность изготовления детали высшего сорта на данном станке равна 0,45. Найдите вероятность того, что среди взятых наудачу 280 деталей половина окажется высшего сорта.
5. В каждой из 1 000 урн находится 5 000 черных и 5 000 белых шаров. Из каждой урны извлекаются без возвращения 3 шара. Чему равна вероятность того, что число урн, из которых извлекли одноцветные шары, заключено между 220 и 300?
6. При бросании трех игральных костей игрок выигрывает 18 руб., если на всех костях выпадет 6 очков; 2 руб. – если на двух костях выпадет 6 очков; 1 руб. – если только на одной кости выпадет 6 очков. Х – величина выигрыша в рублях. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
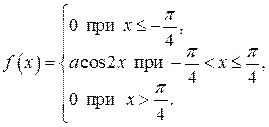
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
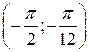. Постройте графики функций распределения и плотности распределения .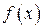
Вариант 16
1. Имеется 5 винтовок, из которых 2 с оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом составляет для данного стрелка 0,95, без оптического прицела – 0,8. Найдите вероятность попадания в цель, если стрелок сделает один выстрел из наудачу взятой винтовки. Пусть при выстреле произошло попадание в цель. Найдите вероятность того, что стреляли из винтовки с оптическим прицелом.
2. При изготовлении радиоламп в среднем бывает 2% брака. Найдите вероятность того, что в партии из 200 ламп не более двух бракованных.
3. Монету бросают 6 раз. Найдите наиболее вероятное число выпадения герба и вероятность появления такого числа гербов.
4. Определите вероятность того, что среди 400 проб руды окажется 275 проб с промышленным содержанием металла, если вероятность промышленного содержания металла одинакова для каждой пробы и равна 0,7.
5. В цехе имеется 80 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени включенными окажутся от 60 до 75 станков.
6. В группе из 5 изделий имеется 1 бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и проверяют. Х – число извлеченных деталей до обнаружения бракованной. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .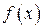
Вариант 17
1. Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05, для второй перфораторщицы эта вероятность равна 0,1. Какова вероятность того, что в наудачу взятом комплекте перфокарт будет найдена ошибка? Какова вероятность того, что эту ошибку допустит: а) первая перфораторщица; б) вторая перфораторщица?
2. Аппаратура содержит 2 000 одинаковых надежных элементов, вероятность отказа для каждого из которых равна 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов?
3. В урне 10 черных и 5 белых шаров. Испытание заключается в следующем: извлекается шар, фиксируется его цвет, возвращается в урну и тщательно перемешивается. Какова вероятность того, что в 3 испытаниях белый шар появится 1 раз?
4. Вероятность того, что деталь выйдет из строя после того как она проработала время t, равна 0,25. Чему равно наиболее вероятное число деталей, вышедших из строя через время t в партии из 50 деталей? Чему равна вероятность появления такого события?
5. Вероятность изготовления детали с номинальными размерами равна 0,7. Вычислите вероятность того, что среди 300 деталей номинальными будут от 200 до 250.
6. На карточках записаны двузначные числа от 31 до 60. Карточку извлекают из урны, фиксируют, возвращают в урну и тщательно перемешивают. Х – число карточек с цифрой 5 в серии из 4 таких испытаний. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .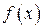
Вариант 18
1. С первого станка на сборку поступает 40%, со второго – 30%, с третьего – 20%, с четвертого – 10% всех деталей. Среди деталей первого станка 0,1% бракованных, второго – 0,2%, третьего – 0,25%, четвертого – 0,5%. Найдите вероятность того, что поступившая на сборку деталь бракованная. Если поступившая на сборку деталь оказалась бракованной, то каким станком вероятнее всего она была изготовлена?
2. По данным ОТК в среднем 3% изделий требуют дополнительной регулировки. Вычислите вероятность того, что из 200 изделий 4 потребуют дополнительной регулировки
3. Вероятность изготовления детали первого сорта равна 0,9. Найдите вероятность того, что из 6 взятых наудачу деталей первого сорта окажется более 4 деталей.
4. Пусть вероятность того, что покупателю необходима обувь 41 размера, равна 0,2. Найдите вероятность того, что из 750 покупателей только 120 потребуют обувь этого размера
5. Из большой партии продукции, содержащей 70% изделий первого сорта, наугад отбирают 100 изделий. Вычислите вероятность того, что среди отобранных будет не менее 50 и не более 90 изделий первого сорта.
6. Имеется 5 патронов. По мишени ведутся выстрелы до первого попадания или пока не будут израсходованы все патроны. Х – число израсходованных патронов. Вероятность попадания при каждом выстреле равна 0,6. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
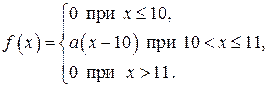
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .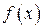
Вариант 19
1. Часы изготавливаются на трех заводах и поступают в магазин. Первый завод производит 40% продукции, второй – 45%, третий – 15%. В продукции первого завода спешат 80% часов, второго – 70%, третьего – 90%. Какова вероятность того, что купленные часы спешат? Если купленные часы спешат, то вероятнее всего на каком заводе они изготовлены?
2. Среди семян ржи 0,4% семян сорняков. Какова вероятность при случайном отборе 500 семян обнаружить 5 семян сорняков?
3. Всхожесть семян некоторого растения составляет 80%. Какова вероятность того, что из 10 посеянных семян взойдут: 9; по крайней мере 8; не менее 9?
4. Вероятность попадания в цель при одном выстреле равна 0,4. Найдите вероятность 100 попаданий из 320 выстрелов.
5. Вероятность выхода конденсатора из строя в течение времени t равна 0,25. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя от 40 до 80 конденсаторов.
6. В партии, состоящей из 10 деталей, имеется 4 бракованных. Наугад извлекают 3 детали. Х – число бракованных деталей среди 3 выбранных. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
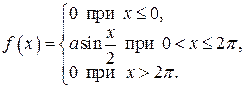
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .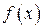
Вариант 20
1. Имеется 10 одинаковых урн, из которых в 9 находится 2 черных и 2 белых шара, а в одной – 5 белых и 1 черный шар. Из наугад взятой урны извлечен шар. Чему равна вероятность того, что этот шар оказался белым? Если шар оказался белым, то какова вероятность того, что он извлечен из урны, содержащей 5 белых шаров?
2. Книга в 1000 страниц имеет 10 опечаток. Какова вероятность того, что на случайно выбранной странице: а) нет опечаток; б) не более трех опечаток?
3. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,1. Найдите вероятность того, что в течение гарантийного срока из 5 телевизоров: не более двух потребуют ремонта; хотя бы 2 потребуют ремонта.
4. На склад магазина поступают изделия, из которых 90% оказываются высшего сорта. Найдите вероятность того, что из 400 взятых наудачу изделий 368 окажутся высшего сорта.
5. При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется от 700 до 820 годных.
6. Вероятность того, что трамвай подойдет к остановке строго по расписанию, равна 0,7. Х – число трамваев, прибывших по расписанию, из 4 исследуемых. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
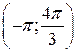. Постройте графики функций распределения и плотности распределения .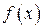
Вариант 21
1. В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В билетах 20 вопросов. Отлично подготовленный студент может ответить на все вопросы, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5 вопросов. Какова вероятность того, что наудачу выбранный студент ответит на 3 произвольно заданных вопроса? Найдите вероятность того, что ответивший на вопросы студент подготовлен: а) отлично; б) плохо.
2. Устройство состоит из 1 000 элементов, работавших независимо один от другого. Вероятность отказа каждого из них в течение времени t равна 0,0025. Найдите вероятность того, что за время t откажут ровно 3 элемента.
3. В цехе 4 мотора. Для каждого мотора вероятность того, что он включен, равна 0,6. Найдите вероятность того, что в данный момент: включено 2 мотора; включены все моторы
4. Батарея дала 140 выстрелов по военному объекту, вероятность попадания в который равна 0,2. Найдите наивероятнейшее число попаданий и его вероятность.
5. Было посажено 400 деревьев. Вероятность того, что отдельное дерево приживется, равна 0,8. Найдите вероятность того, что число прижившихся деревьев больше 300.
6. В лотерее разыгрывается мяч стоимостью 3 руб., шахматы стоимостью 10 руб. и кеды стоимостью 5 руб. Всего билетов 10. Х – величина выигрыша в рублях для лица, имеющего 3 билета. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
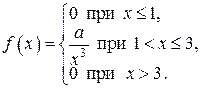
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .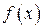
Вариант 22
1. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы четыре студента, из второй – шесть, из третьей – пять студентов. Вероятность того, что отобранный студент из первой, второй, третьей группы попадет в сборную института, равна соответственно 0,5, 0,4 и 0,3. Какова вероятность того, что наудачу взятый студент попадет в сборную? Если студент попал в сборную, то к какой из трех групп он вероятнее всего принадлежит?
2. Пусть вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найдите наиболее вероятное число опоздавших из 855 пассажиров. Какова вероятность того, что опоздает меньше 5 пассажиров?
3. Пусть вероятность того, что покупателю необходима обувь 41 размера, равна 0,3. Найдите вероятность того, что из 5 первых покупателей обувь этого размера будет необходима: одному; по крайней мере одному.
4. Пусть вероятность того, что автомат сработает неправильно, равна 0,3. Найдите наивероятнейшее число случаев неправильной работы автомата при 150 испытаниях. Какова вероятность того, что автомат не сработает такое количество раз?
5. Средний процент нарушений работы кинескопа телевизора в течение гарантийного срока равен 22. Вычислите вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок.
6. Из урны, содержащей 4 белых и 4 черных шара, последовательно извлекают шары до появления первого белого шара, не возвращая их обратно в урну. Х – число извлеченных черных шаров. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.
7. Случайная величина Х задана функцией плотности распределения
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал 
. Постройте графики функций распределения и плотности распределения .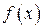
Вариант 23
1. На сборку попадают детали, изготовленные тремя автоматами. Известно, что первый автомат дает 0,4%, второй – 0,2% и третий – 0,6% брака. Найдите вероятность попадания на сборку бракованной детали, если с первого автомата поступило 500, со второго – 1000 и с третьего – 1250 деталей. Если деталь оказалась бракованной, то какой из трех автоматов ее вероятнее всего изготовил?
2. Найдите вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%.
3. На автобазе имеется 10 автомашин. Вероятность выхода на линию каждой из них 0,8. Найдите вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не менее 8 автомашин.
4. На факультете 730 студентов. Вероятность того, что студент не придет на занятия, равна 0,1. Найдите наивероятнейшее число студентов, не явившихся на занятия, и вероятность этого события.
