Элементы стохастического анализа
Виды сходимости последовательности СВ в пространстве.
1) Последовательность СВ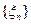 
называется сходящейся почти наверное к СВ 
(
), если
(за исключением быть может 
).
2) Последовательность СВ 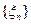называется сходящейся по вероятности к СВ (
), если
.
3) Последовательность СВ 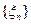называется сходящейся в среднеквадратическомсмысл е к СВ (
), если
.
Из сходимости почти наверное 
сходимость по вероятности. Из сходимости в среднеквадратическом сходимость по вероятности.
.
Мы рассматриваем гильбертовы СП, т.е. для которых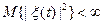 
.
Так как существуют разные виды сходимости для СВ, то соответствующим образом существуют различные виды непрерывности для СП. Кроме того, для различных видов непрерывности (а также дифференцируемости, интегрируемости и др.) имеются соответствующие критерии, которые позволяют установить непрерывность СП (дифференцируемость, интегрируемость и др.).
СП называется непрерывным на Т, если 
. Почти все траектории непрерывного СП являются непрерывными в обычном смысле функциями. Непрерывный СП 
является почти наверное непрерывным в каждой точке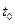 
, 
. Но не наоборот в общем случае.
Непрерывность в смысле сходимости по вероятности называется стохастической непрерывностью; это самый слабый из рассматриваемых видов непрерывности.
СП называется стохастически непрерывным в точке 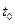, если 
.
Наиболее важной является среднеквадратическая непрерывность.
СП называется среднеквадратически (с.к.-) непрерывным в точке 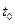, если 
.
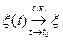СП называется с.к.-непрерывным на Т, если он непрерывен в каждой точке 
.
Теорема. Для с.к.-непрерывности СП в точке необходимо и достаточно, чтобы матожидание было непрерывно в, а корреляционная функция непрерывна в точке.
Из теоремы сразу следует, что 
должна быть непрерывной.
Чтобы исследовать с.к.-непрерывность СП достаточно исследовать непрерывность ее моментных характеристик.
Пример. Пуассоновский процесс.
Пуассоновский процесс имеет следующий физический смысл: при всяком 
величина численно равна количеству событий из простейшего потока интенсивности 
, произошедших к моменту времени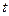 
.
При каждом 
сечение имеет распределение Пуассона с параметром 
: 
СП сходится по вероятности 
, но реализации разрывны. Это происходит потому, что разрывы на каждой реализации в своих точках, и вероятность того, что разрыв будет именно в данной точке 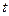равна 0.
Дифференцируемость СП
СВ 
называется с.к.-производной СП в точке 
, если выполняется
.
Если предел существует, то является с.к.-дифференцируемым в точке . Если дифференцируем в каждой точке 
, то говорят, что с.к.-дифференцируем на интервале 
, а семейство СВ 
называется с.к.-производной СП на .
Теорема. Критерий с.к.-дифференцируемости.
