кривые выживания, или их еще называют кривыми дожития, так как отражают зависимость количества доживших до определенного возраста особей от продолжительности этого интервала с самого момента отрождения организмов.
Выделяют три типа основных кривых выживания (рис. 3.1), к которым в той или иной мере приближаются все известные кривые.
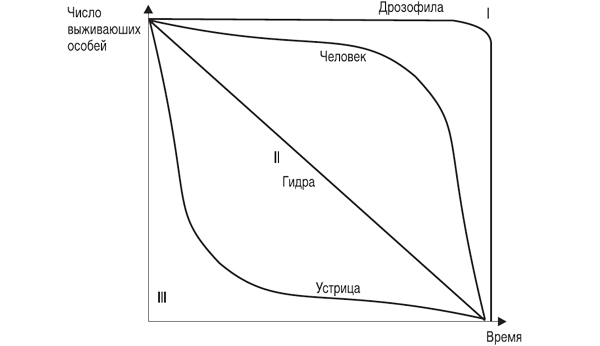
Рис. 3.1. Различные типы кривых выживания (Deevey, 1950)
Кривая I типа, когда на протяжении всей жизни смертность ничтожно мала, резко возрастая в конце нее, характерна для насекомых, которые обычно гибнут после кладки яиц (ее и называют «кривой дрозофилы»), к ней приближаются кривые выживания человека в развитых странах, а также некоторых крупных млекопитающих.
Кривая III типа ¾ это случаи массовой гибели особей в начальный период жизни. Гидробионты и некоторые другие организмы, незаботящиеся о потомстве, выживают за счет огромного числа личинок, икринок, семян и т. п.
Моллюски, прежде чем закрепиться на дне, проходят личиночную стадию в планктоне, где личинки гибнут в огромных количествах, поэтому кривую III называют еще «кривой устрицы».
Кривая II типа (диагональная) характерна для видов, у которых смертность остается примерно постоянной в течение всей жизни. Такое распределение смертности не столь уж редкое явление среди организмов. Встречаются они среди рыб, пресмыкающихся, птиц, многолетних травянистых растений.
Реальные кривые выживания часто представляют собой некоторую комбинацию указанных выше «основных типов». Например, у крупных млекопитающих, да и у людей, живущих в отсталых странах, кривая I вначале круто падает за счет повышенной смертности сразу после рождения.
Модели роста популяций
Экспоненциальный рост
dN/dt = r*N
r - коэф. Размножения.
Предложена Т.Мальтусом в 1798г. Сделано в классическом труде о росте народов населения. Вывод: если так пойдет и дальше, то наступит голод. Так как рост населения превышает рост численности продуктов питания.
Дарвин сделал выводы: поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, которые препятствуют неограниченному размножению. СРЕДИ них нехватка ресурсов и конкуренция с другим видами.
Экспоненциальный рост встречается, но наблюдается короткий период времени.
Ограниченный рост.
dN/dt = r*N*(1- (N/K))
2 свойства: при малых N численность N возрастает экспоненциально, при больших приближается к определенному пределу K; величина называется емкостью K.
2. Логистическая модель Ферхюста.
Породные популяции могут иметь не только максимальную численность, кот определяется емкостью К, но и минимальную численность (=минимально критическую), которая обозначается L. При падении популяции ниже L восстановление, зачастую, не возможно. Пример - китобойный промысел.
3. Математическая биофизика взаимодействующих популяций.
Модель популяции с нижней критической численностью. Зависимость численности популяции о времени и скорости роста от численности.






