Класс
Расстояние L = 120 км автомобиль проехал за время T = 2 часа. Его скорость на первом, хорошем участке пути, была на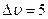 
км/час больше средней скорости, а на втором, плохом участке, на 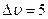км/час меньше средней скорости. Какова длина x хорошего участка пути?
Возможное решение. Средняя скорость автомобиля
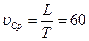км/час. (1)
Скорость автомобиля на первом участке пути
км/час. (2)
Скорость автомобиля на втором участке пути
км/час. (3)
Пусть на преодоление первого участка пути потребовалось время t 1.
Тогда, на преодоление второго участка потребуется время
. (4)
Длина первого участка пути
. (5)
Длина второго участка пути
. (6)
Поскольку
, (7)
это равенство можно, после соответствующих подстановок, привести к виду:
. (8)
Время
час. (9)
Искомая длина
65 км. (10)
Критерии оценивания.
(1) Найдена средняя скорость автомобиля 1 балл
(2) Найдена скорость автомобиля на первом участке пути 1 балл
(3) Найдена скорость автомобиля на втором участке пути 1 балл
(4) Записана связь между 
и 
1 балл
(5) Выражение для длины первого участка пути 1 балл
(6) Выражение для длины второго участка пути 1 балл
(7) Записана связь между 
и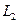 
1 балл
(8) Записано уравнение для нахождения числового значения 1 балл
(9) Найдено время 1 балл
(10) Найдена длина x 1 балл
Задача 2. Система блоков. (Замятнин М.).
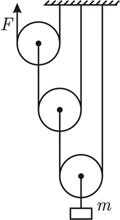
Благодаря механизму, состоящему из лёгких подвижных и неподвижных блоков (рис. 1), соединённых лёгким тросом, можно силой F = 50 Н удерживать груз массой m = 40 кг. Сколько подвижных и неподвижных блоков необходимо для удержания груза? Как устроен такой механизм? Изобразите схему соединения блоков с грузом. Ускорение свободного падения g = 10 Н/кг.
Возможное решение.
Вес груза 
Н. (1)
Система блоков должна дать выигрыш в силе в
раз. (2)
Подвижный блок даёт выигрыш в силе в два раза. (3)
Таким образом, можно использовать четыре подвижных блока, обеспечивающих нужный выигрыш в силе, и ещё три неподвижных блока, для связи подвижных блоков. (4)
Другой способ соединения блоков заключается в следующем: каждый последующий подвижный блок удерживает предыдущий. В этом случае неподвижные блоки не требуются.
Схема соединения блоков в последнем из рассмотренных случаев приведена на рис. 2.
Критерии оценивания.
(11) Найден вес груза 1 балл
(12) Вычислен требуемый выигрыш в силе 1 балл
(13) Преимущество в силе, которое даёт подвижный блок 1 балл
(14) Определено количество подвижных блоков 3 балла
(15) Предложена схема соединений блоков 4 балла
Примечание: За любое правильное решение задачи (независимо от числа использованных блоков) ставится полный балл.
Задача 3. Плавление льда. (Фольклор). В пенопластовом стакане с крышкой лежит лёд. Его температура t Л = 0ºC. В стакан налили такое же количество (по массе) воды, температура которой t В = 20ºC. Сколько процентов льда от первоначального количества осталось в стакане к моменту установления теплового равновесия (выравнивания температуры воды и льда)? Удельная теплоемкость воды С В = 4,2 кДж/(кг·ºC), удельная теплота плавления льда L = 330 кДж/кг.
Возможное решение. К моменту установления теплового равновесия температура воды понизится до t Л = 0ºC. (1)
Запишем уравнение теплового баланса:
m В С В (t В - t Л) = Δ m Л L. (2)
где Δ m Л - масса расплавившегося льда.
Масса расплавившегося льда в стакане (с учётом того, что вначале M Л = m В)
. (3)
Масса оставшегося в стакане льда
m Л = M Л – Δ m Л = 
. (4)
Доля оставшегося льда
74,5% (5)
Критерии оценивания.
(16) Отмечено, что конечная температура смеси равна 0ºC 1 балл
(17) Записано уравнение теплового баланса 3 балла
(18) Получено выражение для массы расплавившегося льда 2 балла
(19) Получено выражение для массы оставшегося льда 2 балла
(20) Найдена доля оставшегося льда (в %) 2 балла
Задача 4. Скорость подъема воды. (Кармазин С.).
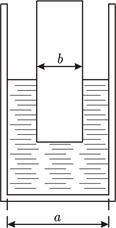
В воду, налитую в стеклянный цилиндрический сосуд квадратного сечения (длина внутренней стороны квадрата a = 10 см) опускают (относительно цилиндра) с постоянной скоростью υo = 8 мм/с стержень квадратного сечения (длина внешней стороны квадрата b = 6 см) (рис. 3). С какой скоростью υ1 поднимается вода в цилиндре?
Возможное решение. Пусть за время t 0 стержень переместился в сторону дна цилиндра на расстояние h 0. При этом он вытеснил объем воды
V 0 = h o b 2. (1)
Вытесненная вода поднялась выше исходного уровня на высоту h 1. Эту высоту найдём из условия:
V 0 = h 1(a 2 – b 2).
Таким образом
(2)
Искомая скорость подъема воды
(3)
После числовой подстановки получим
(4)
Критерии оценивания.
(21) Найден объем воды, вытесняемой за время t 0 2 балла
(22) Высота h 1 на которую поднялась вытесненная вода 3 балла
(23) Приведено выражение для определения скорости подъема воды 3 балла
(24) Получено числовое значение искомой скорости 2 балла
