Теория пределов
Определение
Число А называется пределом функции 
в точке 
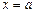, если для сколь угодно малого 
найдется число 
такое, что при 
выполняется 
.
Читается следующим образом:
«Число А называется пределом функции эф от икс в точке икс равное а, если для сколь угодно малого положительного эпсилон найдется число дельта, зависящее от эпсилон, такое, что при модуле разности икс и а меньше дельта выполняется неравенство модуль разности эф от икс и А меньше эпсилон».
Свойства пределов
-
, 
некоторое число. «предел от константы равен самой константе» -
«константу можно выносить за знак предела» -
«предел от суммы равен сумме пределов»
Аналогичное свойство для разности, произведения, частного и т.д.
, 
, 
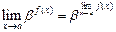
Правило 
, где некоторое число. Например 
Представьте, что Вам необходимо раздать (разделить) одно яблоко огромному (бесконечному) числу людей. В конце концов, от яблока ничего не останется, т.е. нуль.
Следствием этого правила является равенство 
(в теории пределов на нуль делить можно)
Вычисление пределов
1. Вычисление предела начинают с подстановки в функцию значения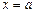
1.1 Пусть 
, 
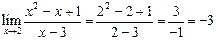
Если Вы получили число, не важно какое: большое или маленькое, целое или дробное, отрицательное или положительное; то это число и является ответом.
1.2 Пусть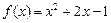 
, 
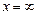
Бесконечность также может являться ответом.
Рассмотрим пример
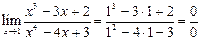
В данном случае мы получили неопределенность.
Основные типы неопределенностей 
В случае получения неопределенности необходимо ее раскрыть с помощью некоторого метода.
Методы раскрытия неопределенностей
2. Деление на наивысшую степень
2.1. 
В данном выражении наивысшая степень х равна 3, следовательно, разделим и числитель и знаменатель на 
.
2.2. 
В данном случае разделим и числитель и знаменатель на 
, т.к. наивысшая степень х равна 5.
3. Разложение на множители
Для того, чтобы разложить многочлен на множители необходимо знать формулы сокращенного умножения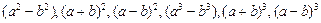 
и уметь делить многочлен на многочлен.
3.1. 
Воспользуемся формулой 
3.2. 
Разделим многочлены в числителе и в знаменателе на (х-2)
Таким образом получим
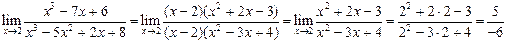
4. Домножение на сопряженное выражение или дополнение до формул сокращенного умножения
Пусть имеется выражение 
, тогда сопряженным выражением будет 
4.1 
Домножим и числитель и знаменатель на сопряженное выражение числителя 
теперь числитель можно упростить по формуле сокращенного умножения 
Получим
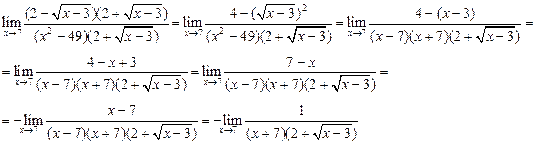
После того как произвели сокращение множителей 
вновь подставляем х=7
Итак получили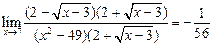 
4.2 
Домножим числитель и знаменатель на 
, чтобы воспользоваться формулой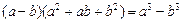 
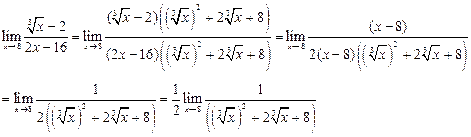
Теперь подставим х=8
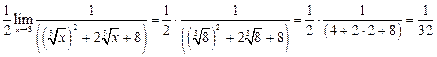
4.3. 
Домножим выражение 
Применим способ делении на наивысшую степень
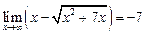
5. Первый замечательный предел
В этом методе необходимо заданный предел привести к виду первого замечательного предела
5.1. 
Домножим числитель и знаменатель на 6
5.2.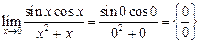 
Воспользуемся формулой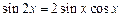 
6. Второй замечательный предел
этот предел имеет неопределенность 
В этом методе необходимо заданный предел привести к виду второго замечательного предела
6.1. 
Для того чтобы данный предел имел вид второго замечательного предела в степени должно быть 
.
теперь выделим второй замечательный предел 
и получим 
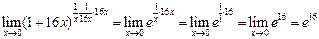
Итак, 
6.2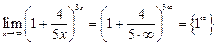 
добавим в степень множитель 
, т.к. 
получим
Итак ответ, 
6.3 
, тогда 
Т.к. 
получим 
Применяя метод деления на наивысшую степень получим 
Ответ 
