Лінійна алгебра
1. Поняття матриці. Види матриць.
2. Операції над матрицями.
3. Сума матриць, властивості суми матриць.
4. Поняття матриці. Транспонування матриць.
5. Добуток матриць. Властивості добутку матриць.
6. Обернена матриця.
7. Визначники другого і третього порядків. Властивості визначників.
8. Визначники п -го порядку. Властивості визначників.
9. Мінори і алгебраїчні доповнення до елементів матриці.
10. Розклад визначника за елементами стовпця або рядка.
11. Загальний вигляд і властивості системи лінійних алгебраїчних рівнянь.
12. Правило Крамера розв’язування систем лінійних алгебраїчних рівнянь.
Аналітична геометрія
13. Загальне рівняння площини. Дослідження неповного рівняння площини.
14. Рівняння площини у відрізках на осях.
15. Рівняння площини, що проходить через три задані точки.
16. Кут між двома площинами. Умова паралельності двох площин.
17. Кут між двома площинами. Умова перпендикулярності двох площин.
18. Відстань від точки до площини.
19. Різні рівняння прямої на площині.
20. Взаємне розміщення двох прямих на площині.
21. Кут прямими на площині.
22. Криві другого порядку
Математичний аналіз
23. Функція: означення і способи задання; області визначення і значень.
24. Класифікація основних елементарних функцій.
25. Числова послідовність: означення і приклади.
26. Границя послідовності: означення і арифметичні дії над збіжними послідовностями.
27. Нескінченно малі та нескінченно великі послідовності і їх властивості.
28. Границя функції: означення і арифметичні дії над функціями, що мають границі.
29. Неперервні функції: означення і арифметичні дії над ними.
30. Неперервність складеної функції.
31. Точки розриву та їх класифікація.
32. Означення похідної та її геометричний та економічний зміст.
33. Правила знаходження похідної суми, добутку і частки двох функцій.
34. Похідна складеної і оберненої функції.
35. Диференційовні функції: означення і зв’язок з існуванням похідної.
36. Похідні обернених тригонометричних функцій  та
та  .
.
37. Похідні обернених тригонометричних функцій  та
та 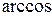 .
.
38. Диференціал функції: означення, обчислення і геометричний зміст.
39. Похідні і диференціали вищих порядків.
40. Правило Лопіталя розкриття невизначеностей „  ” та „
” та „  ”.
”.
41. Формули Тейлора і Маклорена для многочлена і довільної функції.
42. Функції багатьох змінних: означення, область існування, множина значень та графік.
43. Границя функції багатьох змінних.
44. Неперервність функції багатьох змінних.
45. Частинні похідні першого і вищих порядків.
46. Диференційовні функції декількох змінних: означення, повний диференціал.
47. Диференціали вищих порядків функції багатьох змінних.
48. Екстремум функції двох змінних: необхідні і достатні умови.
49. Умовний екстремум функції двох змінних; функція Лагранжа.
Інтегральне числення функції однієї змінної.






