Расчет по образованию трещин нормальных к продольной оси

Расчет по образованию трещин выполняют на расчетные усилия при значении коэффициента надежности по нагрузке 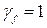; . Расчет по раскрытию трещин не производят, если соблюдается условие

,

где М – изгибающий момент от внешней нагрузки;

M_crc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин

Момент образования трещин предварительно напряженных изгибаемых элементов в стадии эксплуатации определяют по формуле

M_crc = γW_redR_bt,ser + P (e _0p + r).

,

где W_red – момент сопротивления приведенного сечения для крайнего растянутого волокна, определяемый по формуле

r – расстояние от центра тяжести приведенного сечения до верхней ядровой точки, определяется по формуле

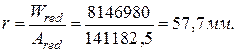
γ =1,3 коэффициент, учитывающий неупругие деформации бетона (табл. П11 приложения).

Так как - трещины в растянутой зоне образуются. Следовательно, необходим расчет по раскрытию трещин.

 

Расчет по раскрытию трещин нормальных к продольной оси

Расчет по раскрытию трещин производят из условия

acrc ≤ acrc,ult,

(2.1)

где a_crc - ширина раскрытия трещин от действия внешней нагрузки; a_crc,ult - предельно допустимая ширина раскрытия трещин.

Для элементов, к которым не предъявляются требования непроницаемости, значения a_crc,ult принимают равными:

- при арматуре классов А240 – А600, В500:

0,3 мм - при продолжительном раскрытии трещин;

0,4 мм - при непродолжительном раскрытии трещин;

- при арматуре классов А800, А1000, а также Вр1200 – Вр1400, К1400, К1500 (К-19) и К1500 (К-7) диаметром 12 мм:

0,2 мм - при продолжительном раскрытии трещин;

0,3 мм - при непродолжительном раскрытии трещин;

при арматуре классов Вр1500 и К1500 (К-7) диаметром 6 и 9 мм

0,1 мм - при продолжительном раскрытии трещин;

0,2 мм - при непродолжительном раскрытии трещин.

Ширину раскрытия трещин принимают равной:

- при продолжительном раскрытии

acrc = acrc 1;

(2.2)

 

- при непродолжительном раскрытии

acrc = acrc 1+ acrc 2- acrc 3,

(2.3)

где a_{crc 1} - ширина раскрытия трещин, определяемая при φ ₁ = 1,4 и при действии постоянных и длительных нагрузок (т. е. при М = M_l);

a_{crc 2}- то же, при φ ₁ = 1,0 и действии всех нагрузок (т.е. при М = M_tot);

a_{crc 3} - то же, при φ ₁=1,0 и действии постоянных и длительных нагрузок (т.е. при М = M_l),Ширину непродолжительного раскрытия трещин можно также определять по формуле

acrc = acrc 2(1+0,4 A), где

(2.4)

 

(2.5)

а значения σ_s, σ_sl, σ_s,crc определяются при действии моментов соответственно M_tot, M_l и М_сrс.

При этом, если выполняется условие A > t, можно проверять только продолжительное раскрытия трещин, а если условие не выполняется - только непродолжительное раскрытие.

Здесь: t = 0,68 - при допустимой ширине продолжительного и непродолжительного раскрытия трещин равных соответственно 0,3 и 0,4 мм;

t = 0,59 - при этих величинах, равных 0,2 и 0,3 мм;

t = 0,42 - при этих величинах равных 0,1 и 0,2 мм.

Ширину раскрытия нормальных трещин определяют по формуле

(2.6)

Пример расчета. Определим приращение напряжения напрягаемой арматуры от действия постоянных и временных длительных нагрузок σ_s = σ_sl т.е. принимая М = M_l = 107,05 кНм.

Поскольку напрягаемая арматура в верхней зоне плиты отсутствует e_{s p} = 0,0, M_s = М_l = 107,05 кН·м и тогда

Рабочая высота сечения равна h _o= 360мм,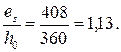

Принимая A'_sp = A_sp = 0,0, имеем

 

Коэффициент приведения равен a_{s 1} = 300/ R_b,ser = 300/18,5 = 16,02, тогда

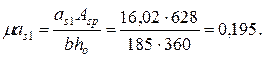
При , φ_f = 0,95 и μa_{s 1} = 0,195 из табл. П12 приложения находим ζ = 0,84, тогда плечо внутренней пары сил z = ζ ·h _о = 0,84·360 = 302,4 мм.

Аналогично определим значение σ_s,crc при действии момента M_s = М_crc = 92,82 кН·м;

При 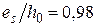, φ_f = 0,95 и μa_{s 1} = 0,195 из табл. П12 приложения находим ζ = 0,85, тогда плечо внутренней пары сил z = ζ ·h о = 0,85·360 = 306 мм.

Аналогично определим значение σ_s, при действии момента M = М_tot = 126,26 кН·м. Поскольку согласно табл. П12 приложения в данном случае при значении e_s / h ₀ >1 коэффициент ζ не зависит от e_s / h ₀, принимаем вычисленное выше значение z = 302,4 мм. При моменте от всех нагрузок М_s = M_tat =126,26 кН·м значение σ_s равно

Проверим условие A > t, принимая t =0,59,

,

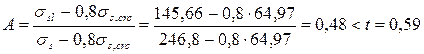следовательно, определяем ширину непродолжительного раскрытия трещин.

Определяем коэффициент ψ_s, принимая σ_s = 246,8 МПа

Определим расстояния между трещинами l_s по формуле

,

где A_bt – площадь зоны растянутого бетона.

Высота зоны растянутого бетона, определенная как для упругого материала, при S_red = 38592299,2 мм³ равна

а с учетом неупругих деформаций растянутого бетона

y_t = k·y₀ = 0,95·124,27= 118,05 мм.

Поскольку y_t > 2 а = 2·40 = 80 мм, принимаем y_t = 118,05 мм. Тогда площадь сечения растянутого бетона равна

A_bt = by_t = 185·118,05 = 21839,25 мм²,

и расстояние между трещинами равно

Поскольку l_s < 400мм и l_s < 40 d = 40·20 = 800 мм, принимаем l_s = 348 мм.

Определяем ширину раскрытия a_{crc, 2}, принимая φ ₁ = 1,0, φ ₂ =0,5

Определяем непродолжительное раскрытие трещин

a_crc = a_{crc, 2} (1 + 0,4 A) = 0,169(1 + 0,4·0,4) = 0,196 мм,

что меньше предельно допустимого значения 0,3 мм.

 

Расчет прогиба плиты

Расчет изгибаемых элементов по прогибам производят из условия

f ≤ fult,

(2.7)

где f - прогиб элемента от действия внешней нагрузки;

f_ult - значение предельно допустимого прогиба.

Прогиб плиты ограничивается эстетическими требованиями.

Для элементов постоянного сечения, работающих как свободно опертые или консольные балки, прогиб допускается определять, вычисляя кривизну только для наиболее напряженного сечения и принимая для остальных сечений кривизны изменяющимися пропорционально значениям изгибающего момента, т.е. по формуле

(2.8)

где - полная кривизна в сечении с наибольшим изгибающим моментом;

S - коэффициент, принимаемый по прил.14.

Полную кривизну изгибаемых элементов определяют:

а) для участков без трещин в растянутой зоне по формуле

(2.9)

где 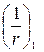и - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок;

- кривизна от непродолжительного действия усилия предварительного обжатия Р (т.е. при действии M = Pe_op).

Кривизну элемента на участке без трещин определяют по формуле

(2.10)

где М - изгибающий момент от внешней нагрузки или момент усилия предварительного обжатия относительно оси, проходящей через центр тяжести приведенного сечения;

I_red - момент инерции приведенного сечения относительно его центра тяжести, определяемый как для сплошного тела по общим правилам сопротивления упругих материалов с учетом всей площади бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону, равным а=E_s /E_{b 1}; E_{b 1}- модуль деформации сжатого бетона, принимаемый равным:

- при непродолжительном действии нагрузки

Eb 1= 0,85 Eb;

(2.11)

- при продолжительном действии нагрузки

(2.12)

б) для участков с трещинами в растянутой зоне по формуле

(2.13)

где - кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям;

- кривизна от непродолжительного действия постоянных и длительных нагрузок;

- кривизна от продолжительного действия постоянных и длительных нагрузок.

Кроме того, в формулах (2.9) и (2.13) может быть учтена кривизна , обусловленная остаточным выгибом элемента вследствие усадки и ползучести бетона в стадии изготовления от усилия предварительного обжатия Р ₍₁₎и собственного веса элемента. Значение определяется по формуле

(2.14)

где σ_sb и σ'_sb - значения, численно равные сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона соответственно для арматуры растянутой зоны и для арматуры, условно расположенной на уровне крайнего сжатого волокна бетона.

Для сечений при h'_f ≤ 0,3 h_o и a'_s < 0,2 h ₀ кривизну допускается определять по формуле

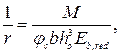
(2.15)

где φ_с - коэффициент, определяемый по прил. 13 в зависимости от φ_f, μa_{s 2}, e_s / h ₀

Пример расчета. Определяем кривизну 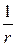в середине пролета от продолжительного действия постоянных и длительных нагрузок, т.е. при М = M_l = 107,05 кН·м.

Для этих нагрузок имеем: 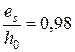, φ_f = 0,95,

При продолжительном действии нагрузки и нормальной влажности имеем 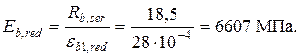ε_{b 1, red} =28×10^-4 при влажности окружающей среды 70 ≥W ≥ 40 %.

Тогда

По табл. П13 приложения при φ_f = 0,95, e_s/h ₀ =1,35 и μα_{s 2} =0,36 находим φ_c =0,61. Тогда кривиз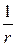на равна

Определим кривизну, обусловленную остаточным выгибом при σ_sb =125,16 МПа.

_1/мм

σ_sb – численно равны сумме потерь напряжений от усадки и ползучести бетона σ_sb = 40+85,16=125,16 МПа.

Полная кривизна в середине пролета от постоянных и длительных нагрузок равна

Прогиб плиты определяем, принимая S =5/48:

Согласно СП 20.13330.2011 «Нагрузки и воздействия» поз.2 при l = 5,84 м предельно допустимый из эстетических требований прогиб равен f_ult = 5840 / 200 =29,2 мм, что превышает вычисленное значение прогиба.