Если 
, 
.
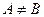Вопрос о значении функции в точке в этом случае не обсуждается, это не имеет смысла, так как всё равно предел не существует, то есть непрерывности быть не может.
Пример.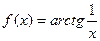 
.
Односторонние пределы для этой функции таковы:
= 
= 
, т.к. если 
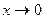и при этом 
то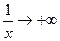 
.
= 
= 
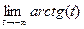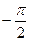, т.к. если 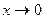и при этом 
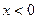то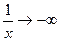 
.
Пример.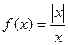 
. Здесь при любом верно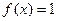 
, а при любом 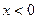верно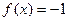 
. В точке 0 односторонние пределы различны.
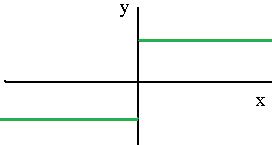
Разрыв 2-го рода.
Если хотя бы один из односторонних пределов не существует или 
, точка называется точкой разрыва 2-го рода.
Примеры 
точка разрыва 
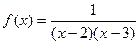точки разрыва 2 и 3.
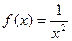. Оба односторонних предела равны 
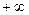, разрыв именно 2 рода а не устранимый, несмотря на совпадение, ведь здесь не конечные числа, а бесконечность. Поэтому нет такой точки вида (0,С) на какой-лиоб конечной высоте, чтобы эта точка устраняла разрыв.
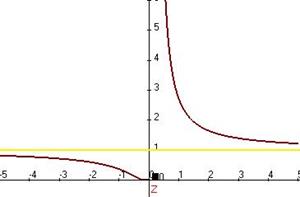
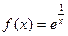. Предел слева равен 0, справа 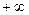. График:
ГЛАВА 6. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.
Введение, основные методы.
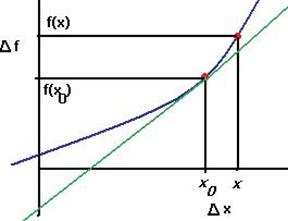
Возьмём две соседние точки на графике некоторой функции. Разность их абсцисс обозначим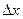 
, а разность ординат 
. Если соединить точки, то получим прямоугольный треугольник, его катеты это именно 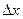и .
Если сближать точки, то можно заметить, что катеты 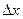и уменьшаются, но угол, в общем случае, не уменьшается к нулю, а стабилизируется. То есть, существует предел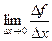 
равный некоторому числу. На этом и основана вся тема, которую мы сейчас будет изучать.
Определение 1.
Производной называется предел отношения приращения функции к приращению аргумента, т.е.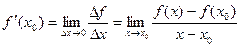 
.
В других обозначениях это же самое можно записать так: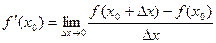 
Геометрический смысл. Так как соотношение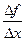 
это тангенс угла наклона секущей, но секущая в пределе стремится к касательной, то производная равна тангенсу угла наклона касательной в графику в точке.
Для векторной функции физический смысл - скорость. Если дано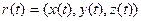 
, то вектор 
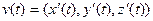это скорость. Этот вектор направлен по касательной к траектории.
Скорость - векторная величина, а скалярная «скорость» измеряемая в км/ч, показываемая в спидометрах на транспорте, это на самом деле - МОДУЛЬ скорости.
Примеры производных для некоторых известных функций.
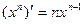в частности 
.
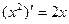Докажем, например, что производная для 2-й степени вычисляется именно по этой формуле.
По определению, 
для этой функции надо записать так: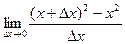 
преобразуем: 
= 
= 
= 
.
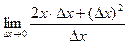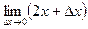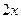Итак, .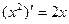
Кстати, тот факт что 
не просто кем-то введено произвольно, а тоже можно доказать: если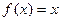 
то = 
= 
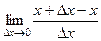= 1.
Аналогично, например, доказывается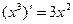 
.
= 
= 
=
= 
= 
.
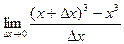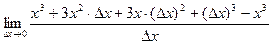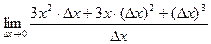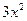Докажем, что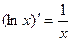 
. 
= 
= 
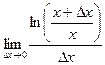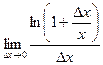Так как следующие бесконечно малые эквивалентны: 
то получим, заменяя на эквивалентную: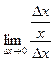 
= 
.
Определение 2.
Функция f называется дифференцируемой в точке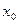 
, если приращение функции можно представить в ви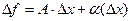де: 
, где 
- бесконечно малая более высокого порядка, чем 1-й.
Действительно, бывают не дифференцируемые функции, например 
не дифф. в нуле. Дело в том, что там нет общей касательной для двух частей графика, правой и левой. Какую бы прямую мы ни провели через (0,0), она не будет касательной к графику функции. Если наклон +450 то есть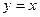 
то разность между ней и левой половиной графика не будет бесконечно-малой: эта прямая является касательной к одной части графика, то она перпендикулярна другой ветви этого же графика.
Взаимосвязь понятий «дифференцируемость» и «производная».
Теорема. Если f есть функция одной переменной, т.е. 
, то существует конечная производная в точке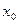 
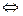функция дифференцируема в точке .
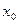Доказательство. Необходимость.
Пусть существует производная в точке, 
. Докажем, что функция дифференцируема. Если 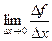равен числу 
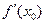, то сама эта функция, которая под знаком предела, представима в виде: это число + какая-то бесконечно малая. 
.
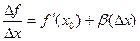Если домножить на 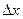то 
. Здесь обозначим 
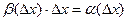, причём эта
более высокого порядка, ведь на уже существующую бесконечно-малую домножается ещё одна, а именно 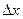, т.е. порядок возрастает на 1. Получили 
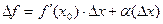. Определение дифференцируемости выполняется.
Достаточность. Пусть f дифференцируема. Выполняется равенство 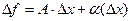. Разделим его на 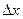: получим 
. Перейдём к пределу. 
.
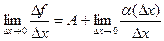Но ведь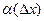 
- бесконечно малая более высокого порядка, то есть там содержится 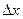не в первой, а какой-то более высокой степени. Тогда 
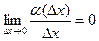. Осталось 
. Заодно доказали, что константа А в этом равенстве - это и есть производная в точке, то есть .
Замечание. В одном из прошлых примеров, а именно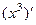 
, элемент 
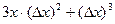это и есть та самая бесконечно малая более высокого порядка 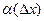. Здесь она содержит 2 и 3 степени, и как видно, даже после деления на 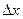она станет 
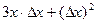, то есть содержит в каждом слагаемом хоть какие-то степени от 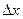, и поэтому стремится к 0.
Лекция № 12. 25. 11. 2016
Лекция № 13. 02. 12. 2016
Лекция № 14. 09. 12. 2016
Лекция № 15. 16. 12. 2016
Лекция № 16. 23. 12. 2016
