Ю. Кузнецов
СПЕЦИАЛЬНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
по курсу
СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ
АВИАЦИОННО-КОСМИЧЕСКИХ СИСТЕМ
РАСЧЕТ ПАРАМЕТРОВ ДВИЖЕНИЯ ЦЕНТРА МАСС
ВСЕАЗИМУТАЛЬНОЙ РАКЕТЫ-НОСИТЕЛЯ
И ВОЗДУШНО-КОСМИЧЕСКОГО САМОЛЕТА
НА УЧАСТКАХ ВЫВЕДЕНИЯ И ВОЗРАТА
Версия 12.00
АННОТАЦИЯ
Специальное программное обеспечение (СПО) обеспечивает моделирование движения центра масс двухступенчатой одноразовой РН или всеазимутальной РН, оснащенной многоразовым крылатым ракетным блоком (КРБ) первой ступени, а также одноступенчатого воздушно-космического самолета (ВКС), комбинированная многорежимная двигательная установка которого включает комбинацию воздушно-реактивных (ВРД) и ракетных двигателей.
Для РН моделирование траектории выведения включает расчет "атмосферной" части участка полета, соответствующей участку полета первой ступени (включая полет по баллистической траектории отделившегося РБ) и «безатмосферной» части, соответствующей участку полета второй ступени. Участок автономного полета КРБ всеазимутальной РН дополнительно включает участок маневра возврата и участок крейсерского полета КРБ в район старта с помощью вспомогательной воздушно-реактивной двигательной установки (ВРДУ). Моделирование траектории выведения ВКС включает расчет "атмосферной" части участка полета, соответствующей участку работы ВРД и «безатмосферной» части, соответствующей участку работы ДУ ВКС в режиме ракетного двигателя.
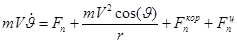 |
Система дифференциальных уравнений, описывающих движение центра масс ЛА в сферически-скоростной системе координат, связанной с вращающейся Землей, имеет следующий вид
 |
 |
(1)
где проекции векторов кориолисовой и переносной сил вычисляются с помощью уравнений (2) и (3).
 =0;
=0;
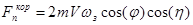 ; (2)
; (2)
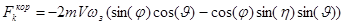 ;
;
и
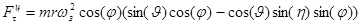 ;
;
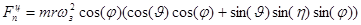 ; (3)
; (3)
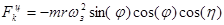 .
.
Вектор равнодействующей внешних сил 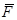 включает в себя:
включает в себя:
-силу притяжения Земли, 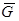 ;
;
-равнодействующую вектора аэродинамических сил, 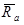 ;
;
-равнодействующую силы тяги ДУ, 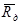 .
.
Составляющие ускорения силы притяжения в сферической системе координат рассчитываются по следующим формулам
 ;
;
 ; (4)
; (4)
 ,
,
где
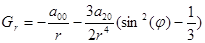
 . (5)
. (5)
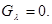
Составляющие равнодействующей вектора аэродинамических сил 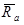 в скоростной системе включают:
в скоростной системе включают:
-силу лобового сопротивления X;
-подъемную силу Y;
-боковую силу Z.
При моделировании полета ЛА в атмосфере используется ряд допущений:
-система управления обеспечивает ориентацию вектора скорости в плоскости тангажа;
-угловые скорости по углам атаки и крена малы, вследствие чего перекрестные аэродинамические связи между каналами тангажа, рыскания и крена отсутствуют;
-координаты центра масс и центра давления лежат в плоскости тангажа.
Перечисленные допущения позволяют при моделировании пространственного движения ЛА в атмосфере не учитывать его аэродинамические характеристики по углу скольжения и за счет этого сократить в два раза объем аэродинамических данных для ЛА типа крылатых ракетных блоков, не обладающих в отличие от обычных РН аэродинамической симметрией по углам  и
и 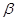 .
.
Проекции силы лобового сопротивления и подъемной силы на оси скоростной системы координат имеют следующий вид
 ;
;
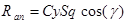 ; (6)
; (6)
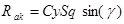 ,
,
где q – скоростной напор;
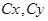 - коэффициенты силы лобового сопротивления и подъемной силы, отнесенные к характерной площади (для РН – это площадь миделя, для КРБ – площадь крыла);
- коэффициенты силы лобового сопротивления и подъемной силы, отнесенные к характерной площади (для РН – это площадь миделя, для КРБ – площадь крыла);
 - скоростной угол крена (угол крена относительно местной вертикали).
- скоростной угол крена (угол крена относительно местной вертикали).
При расчете составляющих аэродинамических сил последние рассчитываются как произведение коэффициентов силы лобового сопротивления и подъемной силы от угла атаки: 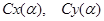 и изменения приведенного коэффициента силы лобового сопротивления и подъемной силы или аэродинамического качества от числа Маха:
и изменения приведенного коэффициента силы лобового сопротивления и подъемной силы или аэродинамического качества от числа Маха:  . Нахождение текущего значения параметров Сх, Су, К обеспечивается путем линейной интерполяции таблично заданных значений соответствующих параметров.
. Нахождение текущего значения параметров Сх, Су, К обеспечивается путем линейной интерполяции таблично заданных значений соответствующих параметров.
Эксплуатационные параметры ВРД рассчитываются путем линейной интерполяции таблично заданных в виде двумерных массивов в функции числа Маха и высоты полета высотно-скоростных характеристик двигателя:
- относительной тяги  , где
, где 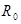 - тяга двигателя на стенде на номинальном режиме (М=0, Н=0,
- тяга двигателя на стенде на номинальном режиме (М=0, Н=0, 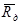 =1.0);
=1.0);
- относительного удельного расхода топлива 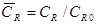 , приведенного к удельному расходу топлива на стенде на номинальном режиме (М=0, Н=0,
, приведенного к удельному расходу топлива на стенде на номинальном режиме (М=0, Н=0, 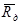 =1.0);
=1.0);
-дроссельной характеристики С R (R).
Потери тяги обусловленные установкой ДУ на ЛА учитываются путем введения поправочных коэффициентов, учитывающих характеристики выбранного варианта воздухозаборника и сопла в функции числа Маха Квз.(М) и Кс.(М).
Таким образом, тяга, удельный и секундный расход топлива без учета потерь в воздухозаборнике и сопле могут быть рассчитаны через обобщенные параметры по следующим зависимостям:
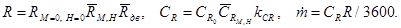
где 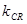 - коэффициент, учитывающий изменение экономичности двигателя при его дросселировании,
- коэффициент, учитывающий изменение экономичности двигателя при его дросселировании, 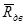 - режим работы ДУ в долях номинала.
- режим работы ДУ в долях номинала.
Управление ЛА на атмосферном участке полета производится изменением угла атаки  , при этом конструктивные особенности ЛА учитываются путем выставки равнодействующей вектора тяги ДУ в вертикальной плоскости
, при этом конструктивные особенности ЛА учитываются путем выставки равнодействующей вектора тяги ДУ в вертикальной плоскости 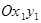 связанной системы координат на угол атаки
связанной системы координат на угол атаки 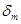 . Управление ЛА на безатмосферном участке полета производится изменением угла тангажа, который затем пересчитывается в угол атаки,
. Управление ЛА на безатмосферном участке полета производится изменением угла тангажа, который затем пересчитывается в угол атаки,
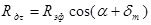 ;
;
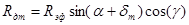 ; (7)
; (7)
 ,
,
где  - эффективная тяга ДУ, определяемая для ВРД как разность между идеальной тягой собственно двигателя (
- эффективная тяга ДУ, определяемая для ВРД как разность между идеальной тягой собственно двигателя (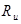 ) и потерями (
) и потерями (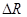 ), обусловленными установкой двигателя на конкретный вариант ЛА, нерасчетными режимами работы ДУ и пр. Для ЖРД потери эффективной тяги не учитывают, а влияние донного давления учитывается при задании аэродинамических характеристик второй ступени РН.
), обусловленными установкой двигателя на конкретный вариант ЛА, нерасчетными режимами работы ДУ и пр. Для ЖРД потери эффективной тяги не учитывают, а влияние донного давления учитывается при задании аэродинамических характеристик второй ступени РН.
Функционально модель движения центра масс ЛА включает четыре программы моделирующие соответственно:
-движение центра масс ВКС на "атмосферном" участке полета и КРБ на участке крейсерского полета;
-движение центра масс первой ступени РН на "атмосферном" участке полета;
-движение ВКС и второй ступени РН на "безатмосферном" участке полета;
-пространственное движение центра масс КРБ на участке маневра возврата.
Такое разделение объясняется существенными различиями в законах управления, реализуемых на "атмосферной" и "безатмосферной" части участка выведения, а также различиями в динамике полета ВКС, КРБ и РН в атмосфере.
Например, при расчете параметров движения ЦМ ВКС на участке работы ВРД и КРБ на участке крейсерского полета принята идеология «программированного» движения, реализуемая путем моделирования отдельных типовых операций, на которых с помощью таблицы формируются полетные режимы и аэродинамическая конфигурация ЛА, определяемая положением шасси и закрылков, режимы работы ДУ, настройки автомата стабилизации и моделирующей программы. В частности, программа полета ВКС на атмосферной части участка выведения включает: разбег, выдерживание, уборку шасси, уборку взлетно-посадочной механизации, набор высоты, маневр прохождения трансзвука, выход на режим и полет с постоянным скоростным напором и маневр по тангажу перед запуском ЖРД.
При моделировании "атмосферного" и "безатмосферного" участков полета РН и участке работы ЖРД ВКС, проходящем в верхних слоях атмосферы и космосе, реализуются жесткие временные программы управления углами атаки и тангажа (т.е. углом между продольной осью ЛА ох1 и плоскостью местного горизонта).

 |
В свою очередь пространственное движение КРБ на участке маневра возврата обеспечивается путем задания опорной программы управления углом атаки в функции числа Маха и выбором соответствующих законов управления углами атаки и крена в модели автомата стабилизации, обеспечивающих выдерживание заданного комплекса ограничений, налагаемых н траекторные параметры и режимы нагружения конструкции 
КРБ.
При моделировании движения ЛА по ВПП в процессе разбега или пробега, исходная система уравнений заменяется упрощенной системой, состоящей из двух дифференциальных уравнений, описывающих движение центра масс ЛА по плоской поверхности без уклона
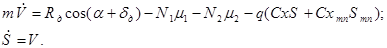 (8)
(8)
Нагрузки на носовую и главные стойки шасси (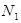 и
и 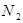 ) определяются путем решения системы линейных уравнений
) определяются путем решения системы линейных уравнений
 ;
;
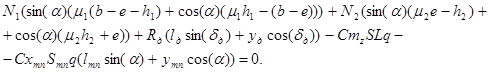 (9)
(9)
Последнее из уравнений представляет собой условие равенства моментов внешних сил относительно центра масс ЛА,
где 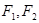 - силы трения качения пневматиков носовой и главных стоек шасси, равные соответственно:
- силы трения качения пневматиков носовой и главных стоек шасси, равные соответственно: 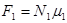 ,
,  ;
;
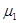 ,
,  - коэффициенты трения качения (для сухого бетонного покрытия и незаторможенных колес:
- коэффициенты трения качения (для сухого бетонного покрытия и незаторможенных колес:  =0.04, для заторможенных:
=0.04, для заторможенных:  =0.25-0.30);
=0.25-0.30);
 - расстояние от поверхности ВПП до продольной оси ЛА при обжатых амортизаторах;
- расстояние от поверхности ВПП до продольной оси ЛА при обжатых амортизаторах;
 – база и вынос колес главных стоек шасси относительно центра масс;
– база и вынос колес главных стоек шасси относительно центра масс;
 - координаты ДУ и угол ориентации вектора тяги относительно продольной оси ЛА;
- координаты ДУ и угол ориентации вектора тяги относительно продольной оси ЛА;
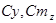 - коэффициент подъемной силы и коэффициент момента тангажа относительно центра масс ЛА;
- коэффициент подъемной силы и коэффициент момента тангажа относительно центра масс ЛА;
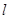 - характерная длина ЛА;
- характерная длина ЛА;
 - координаты узла крепления тормозного парашюта в БСК;
- координаты узла крепления тормозного парашюта в БСК;
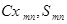 - коэффициент Cx и площадь тормозного парашюта;
- коэффициент Cx и площадь тормозного парашюта;
 - угол атаки.
- угол атаки.
Внимание
При аварийном останове, вызванном ошибками пользователя при изменении исходных данных, для восстановления ИД скопировать соответствующий файл НУ из каталога «нсходные НУ» и отредактировать его расширение.
Если параметр в версии 12.00 не используется, - его значение в ИД не изменять!






