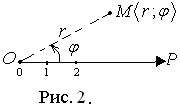 Положение точки М в ПСК (рис. 2) определяют две координаты: М
Положение точки М в ПСК (рис. 2) определяют две координаты: М  , где r – полярный радиус (r = |0M|), φ =
, где r – полярный радиус (r = |0M|), φ = 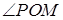 – полярный угол.
– полярный угол.
ОДЗ для полярных координат: 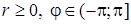 или
или 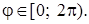
Если совместить ПСК и ДСК так, чтобы полюс совпал с началом
координат ДСК, а ось ОР совпадала с положительной полуосью ОХ,
то получим формулы связи между декартовыми координатами точки M (x; y)
и ее полярными координатами М 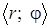 :
:
 и
и 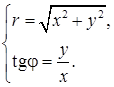 (4)
(4)
Чтобы найти полярный угол φ по известному значению tgφ, нужно учесть, в какой четверти координатной плоскости находится точка М:
 (5)
(5)
В ПСК уравнение линии имеет вид F (r, φ) = 0 или r = f (φ).
Прямая линия на плоскости
 Общее уравнение прямой на плоскости:
Общее уравнение прямой на плоскости:
Ах + В у + С = 0.
Уравнение прямой с угловым коэффициентом (рис. 3):
у = k x + b. (6)
Уравнение вертикальной прямой (рис. 3):
х = а. (7)
Уравнения прямых, проходящих через одну заданную точку М (х 0; у 0) (уравнение пучка прямых):
у – y 0 = k (x – x 0). (8)
Угловой коэффициент прямой, проходящей через две заданные точки А (х 1; у 1) и В (х 2; у 2):
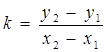 . (9)
. (9)
Уравнение прямой, проходящей через две заданные точки:
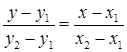 . (10)
. (10)
Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k 1 x + b 1 и у = k 2 x + b 2.
Условие параллельности прямых на плоскости:
k 1 = k 2. (11)
Условие перпендикулярности прямых:
 . (12)
. (12)
Если одна из двух перпендикулярных прямых вертикальная, т.е. k 2 не существует, то k 1 = 0 и обратно: если k 2 = 0, то k 1 не существует.
Тангенс острого угла между пересекающимися прямым и можно найти, используя формулу:
 , (13)
, (13)
откуда  . Если одна из прямых вертикальная, т.е. k 2 не существует, то
. Если одна из прямых вертикальная, т.е. k 2 не существует, то 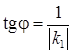 .
.
Кривые второго порядка
 Каноническое уравнение эллипса:
Каноническое уравнение эллипса:
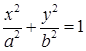 . (14)
. (14)
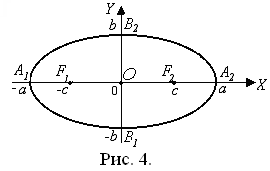
Термины и обозначения основных элементов эллипса (рис. 4):
O – центр эллипса;
с – фокусное расстояние;
F 1(–c; О), F 2(c; О) – фокусы эллипса;
| А 1 А 2 | = 2 a – длина большой оси;
а – большая полуось эллипса;
|B 1 B 2 | = 2 b – длина малой оси;
b – малая полуось эллипса.
Для эллипса справедливо: c 2 = a 2 – b 2.
Число  называется эксцентриситетом эллипса
называется эксцентриситетом эллипса 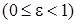 .
.
Если a < b, то эллипс имеет вытянутую по вертикали форму (рис. 5).
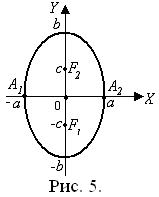 В этом случае фокусы эллипса F 1(О; –c), F 2(О; c),эксцентриситет
В этом случае фокусы эллипса F 1(О; –c), F 2(О; c),эксцентриситет  и справедливо c 2 = b 2 – a 2.
и справедливо c 2 = b 2 – a 2.
Если a = b, то уравнение эллипса становится уравнением окружности:
x 2 + y 2 = R 2,
где R= a= b.
В этом случае фокусы эллипса совпадают с центром окружности, фокусное расстояние с = 0, эксцентриситет окружности  .
.
Каноническое уравнение гиперболы:
 . (15)
. (15)
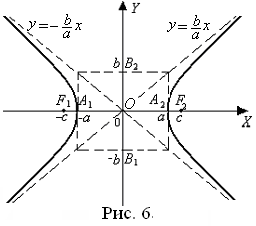 Термины и обозначения основных элементов гиперболы (рис. 6):
Термины и обозначения основных элементов гиперболы (рис. 6):
O – центр гиперболы;
с – фокусное расстояние;
F 1(–c; 0), F 2(c; 0) – фокусы гиперболы;
| А 1 А 2 | = 2 a – длина вещественной оси;
а – вещественная полуось гиперболы;
|B 1 B 2 | = 2 b – длина мнимой оси;
b – мнимая полуось гиперболы.
Уравнения асимптот гиперболы:
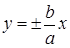 .
.
Для гиперболы справедливо: с 2 = a 2 + b 2.
Число  называется эксцентриситетом гиперболы
называется эксцентриситетом гиперболы  .
.
Канонические уравнения параболы.
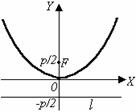 Рис. 7
Рис. 7
| Существуют 4 вида канонических уравнений параболы:
х 2 = 2 ру. (16)
Фокус F (0; 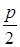 ), уравнение директрисы: у = – ), уравнение директрисы: у = – 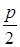 .
х 2 = – 2 ру. (17)
Фокус F (0; – .
х 2 = – 2 ру. (17)
Фокус F (0; – 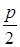 ), уравнение директрисы: у = ), уравнение директрисы: у = 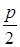 .
у 2 = 2 рх. (18)
Фокус F ( .
у 2 = 2 рх. (18)
Фокус F (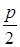 ; 0), уравнение директрисы: х = – ; 0), уравнение директрисы: х = – 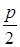 .
у 2 = – 2 рх. (19)
Фокус F (– .
у 2 = – 2 рх. (19)
Фокус F (– 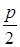 ; 0), уравнение директрисы: х = ; 0), уравнение директрисы: х = 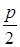 . .
|
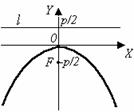 Рис. 8
Рис. 8
| |
 Рис. 9
Рис. 9
| |
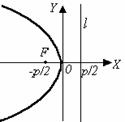 Рис. 10
Рис. 10
|
Термины и обозначения основных элементов параболы: O – вершина параболы, F – фокус параболы, p – параметр параболы (расстояние от фокуса F до директрисы l).
Для приведения уравнения кривой со смещенным центром к каноническому виду может быть использован параллельный перенос системы координат в точку O 1(α; β).При параллельном переносе координаты любой точки М (х; у) в новой системе координат X 1 O 1 Y 1 будут (х 1; у 1), где
 (20)
(20)
Примеры таких преобразований приведены в табл. 2.
Таблица 2
| В системе координат ХОY | В системе координат X 1 O 1 Y 1 |
Окружность с центром в точке O 1(α;β) и с радиусом R:

| Каноническое уравнение окружности:
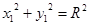
|
Эллипс с центром в точке O 1(α;β ):
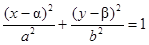
| Каноническое уравнение эллипса:

|
Гипербола с центром в точке O 1(α;β): 
| Каноническое уравнение гиперболы:  . .
|
Параболы с вершиной в точке O 1(α;β)  или
или 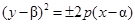 . .
| Канонические уравнения парабол:
 или или 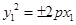
|
Примерный вариант и образец выполнения
контрольной работы № 1
Задача 1. Даны координаты вершин треугольника АВС: А (–3; –1),
В (4; 6), С (8; –2).
Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А (3; 0), уравнение прямой l: 3 x = 4
и число λ = 3: 2.
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка: 
+ 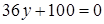 .
.
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка 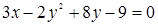
и уравнение прямой l: x + 2 y – 3 = 0.
Требуется:
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК):
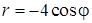 .
.
Требуется:
1) найти область определения функции  ;
;
2) построить кривую в ПСК, вычислив значения функции в точках 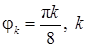 = 0, 1,..., 16, принадлежащих области определения функции
= 0, 1,..., 16, принадлежащих области определения функции 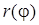 ;
;
3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Решение задачи 1
1) Вычислим длину стороны ВС по формуле (1):
| BС | =  =
=
= 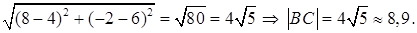
2) Составим уравнение стороны ВС, используя формулу (10):
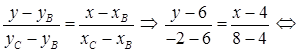
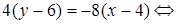
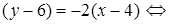 y = –2 x + 14 – уравнение ВС.
y = –2 x + 14 – уравнение ВС.
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (9):

и возьмем из уравнения ВС угловой коэффициент прямой ВС:  .
.
Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (13) вычислим

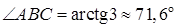 .
.
4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (8) и условие перпендикулярности прямых (12). Сначала вычислим угловой коэффициент прямой АK. Так как 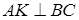 , то
, то  .
.
Уравнение AK получим по формуле (8):
у – уА = kAK (x– xA) 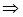 у – (– 1) =
у – (– 1) = 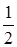 (x– (– 3))
(x– (– 3)) 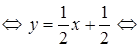
x – 2 y + 1 = 0 – уравнение AK.
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2: 1, начиная от точки А, т. е.  .
.
Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):

 М (6; 2).
М (6; 2).
Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении 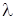 = 2, начиная
= 2, начиная
от точки А, по формулам деления отрезка в заданном отношении (2):



P (3; 1) – центр тяжести треугольника АВС.
6) Построим чертеж к задаче в системе координат ХОY (рис. 11). Полученные при решении задачи результаты не противоречат чертежу.
 Ответы:
Ответы:
1) длина стороны | BС| =  ;
;
2) уравнение стороны ВС:
y = – 2 x + 14;
3) угол при вершине В:  ;
;
4) уравнение высоты АK: x – 2 y +
+ 1= 0;
5) координаты центра тяжести треугольника P (3; 1);
6) чертеж на рис. 11
Решение задачи 2
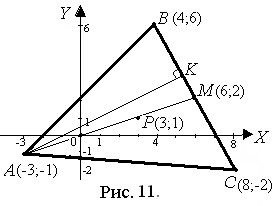
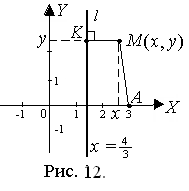 Пусть М (х; у) – произвольная точка на координатной плоскости, удовлетворяющую условию задачи (рис. 12), т. е.
Пусть М (х; у) – произвольная точка на координатной плоскости, удовлетворяющую условию задачи (рис. 12), т. е. 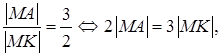 где K – основание перпендикуляра, опущенного из точки М на прямую 3 x = 4. Так как K лежит
где K – основание перпендикуляра, опущенного из точки М на прямую 3 x = 4. Так как K лежит
на прямой 3 x = 4, то 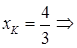 K
K  .
.
Запишем условие  в координатной форме, используя формулу (1) для длины отрезка:
в координатной форме, используя формулу (1) для длины отрезка:
 .
.
Это и есть уравнение искомой траектории, так как ему удовлетворяют координаты любой точки М (х; у) на этой траектории.
Для упрощения уравнения возведем обе части равенства в квадрат
и приведем подобные члены:
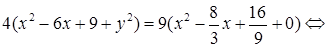

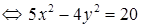 ,
,
откуда получаем
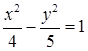 – уравнение гиперболы с полуосями
– уравнение гиперболы с полуосями
 .
.
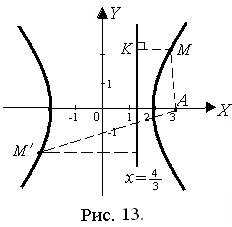 Построим чертеж гиперболы в системе координат ХОY (рис. 13).
Построим чертеж гиперболы в системе координат ХОY (рис. 13).
Ответ: 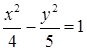 – уравнение траектории. Чертеж на рис. 13.
– уравнение траектории. Чертеж на рис. 13.
Решение задачи 3
Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим в уравнении полные квадраты по переменным х и у:
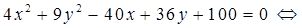
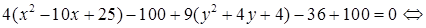
 .
.
Получили уравнение эллипса с центром в точке O 1(5; –2) (см. табл. 2
в разделе "справочный материал").
Осуществив параллельный перенос осей координат в системе XOY
по формулам:  получим каноническое уравнение эллипса
получим каноническое уравнение эллипса  в системе координат X 1 O 1 Y 1, где O 1(5; –2) в системе XOY (рис. 14).
в системе координат X 1 O 1 Y 1, где O 1(5; –2) в системе XOY (рис. 14).
Найдем характерные элементы эллипса: 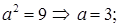
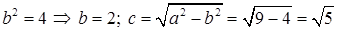 .
.
Отсюда получаем: а = 3 – большая полуось эллипса, b = 2 – малая полуось эллипса, с =  – фокусное расстояние. Координаты фокусов эллипса в системе координат X 1 O 1 Y 1: F 1(–
– фокусное расстояние. Координаты фокусов эллипса в системе координат X 1 O 1 Y 1: F 1(–  ; 0), F 2(
; 0), F 2( ; 0).
; 0).
Найдем координаты фокусов в системе координат XOY:
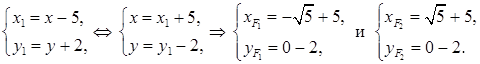
Таким образом, координаты фокусов эллипса в системе координат XOY:
F 1(– 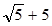 ; – 2), F 2(
; – 2), F 2(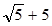 ;–2).
;–2).
Вычислим эксцентриситет эллипса: 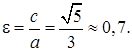
 Изобразим на чертеже расположение эллипса относительно обеих систем координат (рис. 14).
Изобразим на чертеже расположение эллипса относительно обеих систем координат (рис. 14).
Ответ: 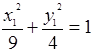 – каноническое уравнение эллипса, где
– каноническое уравнение эллипса, где 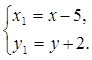
Характерные элементы:
– O 1(5; –2) – центр эллипса;
– а = 3 – б большая полуось эллипса, b = 2 – малая полуось эллипса;
– с = 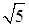 – фокусное расстояние;
– фокусное расстояние;
– координаты фокусов эллипса в системе координат XOY: F 1(– 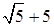 ; – 2), F 2(
; – 2), F 2(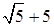 ; –2);
; –2);
– эксцентриситет эллипса 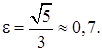
Чертеж на рис. 14.
Решение задачи 4
1) Приведем заданное уравнение кривой 2-го порядка к каноническому виду. Для этого выделим полный квадрат по переменной у (квадрат переменной х в уравнении отсутствует):

 .
.
Получили уравнение параболы вида  с вершиной
с вершиной
в точке  (см. табл. 2 в разделе "справочный материал"). Осуществим параллельный перенос осей координат по формулам:
(см. табл. 2 в разделе "справочный материал"). Осуществим параллельный перенос осей координат по формулам: 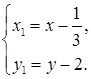
В результате получим каноническое уравнение параболы 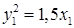 в системе координат X 1 O 1 Y 1.
в системе координат X 1 O 1 Y 1.
2) Найдем точки пересечения параболы и заданной прямой в системе координат XOY. Для этого решим систему уравнений:

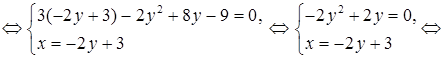


Таким образом, парабола и прямая пересекаются в точках А (3; 0)
и В (1; 1).
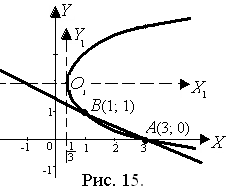 3) Построим обе линии в системе координат XOY (рис. 15).
3) Построим обе линии в системе координат XOY (рис. 15).
Ответы: 1) 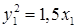 ;
;
2) А (3; 0), В (1; 1);
3) чертеж на рис. 15.
Решение задачи 5
1) Область определения функции 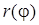 найдем из условия
найдем из условия 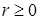 :
:

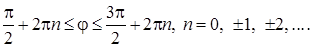
При n = 0 получаем  при
при 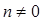 интервалы
интервалы  Следовательно, область определения
Следовательно, область определения 
2) Для построения кривой в ПСК вычислим значения функции 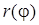
в точках  0, 1, …, 16, входящих в область определения, т. е.
0, 1, …, 16, входящих в область определения, т. е.
в точках, где выполнено условие  , и заполним табл. 3.
, и заполним табл. 3.
Таблица 3
| k | 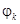
| 
| k | 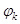
| 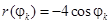
|
| – | – | – | – | ||
| π/8 | – | 9π/8 | 3,7 | ||
| 2π/8 | – | 10π/8 | 2,8 | ||
| 3π/8 | – | 11π/8 | 1,5 | ||
| 4π/8 | 12π/8 | ||||
| 5π/8 | 1,5 | 13π/8 | – | ||
| 6π/8 | 2,8 | 14π/8 | – | ||
| 7π/8 | 3,7 | 15π/8 | – | ||
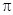
| 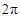
| – |
 Для построения точек кривой в ПСК
Для построения точек кривой в ПСК
в каждом из направлений, задаваемых углом 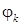 , откладываем от полюса отрезок длины
, откладываем от полюса отрезок длины  . Соединив полученные таким образом точки, получаем график функции
. Соединив полученные таким образом точки, получаем график функции 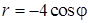 в ПСК (рис. 16).
в ПСК (рис. 16).
3) Найдем уравнение кривой, заданной в ПСК уравнением 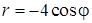 , в декартовой системе координат.
, в декартовой системе координат.
Если совместить ПСК и ДСК так, чтобы полюс совпал с началом координат ДСК, а ось ОР совпадала с положительной полуосью ОХ, то, используя формулы связи между декартовыми и полярными координатами точки 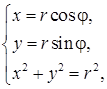 получим:
получим: 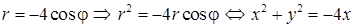 .
.
Следовательно, уравнение кривой 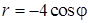 в ДСК имеет вид уравнения кривой 2-го порядка:
в ДСК имеет вид уравнения кривой 2-го порядка: 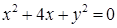 .
.
4) Для определения типа кривой выделим в уравнении полные квадраты по переменным х и у:
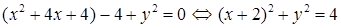 .
.
Это уравнение задает окружность с центром в точке O 1(–2; 0) и с радиусом R = 2. Найдем координаты точки O 1(–2; 0) в ПСК:

 ,
,
(здесь выбираем n = 1, так как 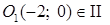 четверти (формулы (5)).
четверти (формулы (5)).
Ответы:
1) область определения: 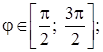
2) чертеж на рис. 16;
3) уравнение кривой в ДСК: 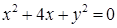 ;
;
4) тип кривой – окружность с центром в точке 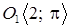 и с радиусом R = 2.
и с радиусом R = 2.
Справочный материал по темам
"Элементы линейной алгебры. Аналитическая
геометрия в пространстве"
Матрицы
Матрицей размерности m ´ n называется прямоугольная таблица, состоящая из m·n элементов (m строк и n столбцов):
Am ´ n = 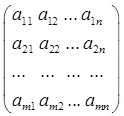 ,
,
где aij – элементы матрицы, i = 1, 2, …, m – номер строки, j = 1, 2, …,
n – номер столбца.
Для краткости матрицу обозначают одной буквой, например, буквой А.
Некоторые виды матриц:
1) нулевая матрица: матрица, все элементы которой равны нулю;
2) при n = 1 матрица-столбец: X =  ;
;
3) при m = 1 матрица-строка: Y =  ;
;
4) при m = n квадратная матрица: An ´ n = 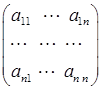 .
.
У квадратной матрицы различают главную диагональ (соединяющую элементы a 11 и ann) и побочную диагональ.
Примеры квадратных матриц:
1) единичная матрица (квадратная матрица, на главной диагонали которой стоят единицы, а остальные элементы – нули):
E =  ;
;
2) квадратная матрица второго порядка: 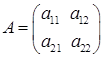 ;
;
3) квадратная матрица третьего порядка: 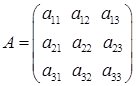 .
.
Две матрицы А и В называются равными, если они имеют одинаковые размерности и их соответствующие элементы равны:
Am´n = Bm´n Û aij = bij (i = 1, 2, …, m; j = 1, 2, …, n).






