Раздел 2 Первый закон термодинамики

Смеси идеальных газов

Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газо­вую постоянную, молекулярную массу и теплоемкость смеси.

Закон Дальтона. В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов:

Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси. Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

.

Очевидно, что и .

Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .

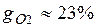Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .

Приведенным называется объем, который занимал бы компонент газа, ес­ли бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i -го компонента:

; (2.1)

.

Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает пол­ный объем смеси, а второе уравнение — к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона ,откуда . Объемные доли также часто задаются в процентах. Для воз­духа , .

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей вто­рого компонента и т. д. Число молей смеси , а мольная доля компонента будет равна .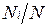

В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. 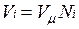а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.

Газовая постоянная смеси газов. Просуммировавуравнения (2.1) для всех компонен­тов смеси, получим . Учитывая , можно записать

, (2.3)

где

. (2.4)

Из уравнения (2.3) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона. Поскольку то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид

(2.5)

Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси : (2.6)

Сравнивая правые части соотношений (2.5) и (2.6), найдем

.

Изопределения массовых долей следует, что

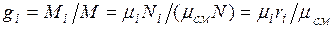
Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:

. (2.7)

Соотношение между объемными и массо­выми долями. Учитывая (2.7), получаем .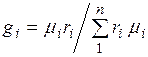

Поскольку , то

Разделив числитель и знаменатель этой формулы на массу смеси М, получим

.

Аналитическое выражение первого закона термодинамики

Первый закон термодинамики пред­ставляет собой частный случай всеобще­го закона сохранения и превращения энергии применительно к тепловым явле­ниям. В соответствии с уравнением Эйн­штейна 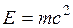надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон со­хранения энергии можно рассматривать независимо.

Закон сохранения и превращения энергии является фундаментальным за­коном природы, который получен на ос­нове обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утвер­ждает, что энергия не исчезает и не воз­никает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.

В числе первых ученых, утверждав­ших принцип сохранения материи и энер­гии, был наш соотечественник М. В. Ло­моносов (1711 — 1765 гг.).

Пусть некоторому рабочему телу с объемом V и массой М, имеющему тем­пературу Т и давление р, сообщается из­вне бесконечно малое количество тепло­ты . В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.

Повышение температуры тела свиде­тельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциаль­ной энергии частиц. В результате внут­ренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него дав­ление, то при расширении оно произво­дит механическую работу против сил внешнего давления. Так как никаких других изменений в системе не происхо­дит, то по закону сохранения энергии

(2.8)

т. е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.

Полученное уравнение является ма­тематическим выражением первого зако­на термодинамики. Каждый из трех чле­нов этого соотношения может быть поло­жительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.

1. — теплообмен системы с ок­ружающей средой отсутствует, т. е. теп­лота к системе не подводится и от нее не отводится. Процесс без теплообмена на­зывается адиабатным. Для него уравнение (2.8) принимает вид:

.

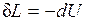Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабат­ном сжатии рабочего тела затрачивае­мая извне работа целиком идет на увели­чение внутренней энергии системы.

2. — при этом объем тела не изменяется, dV =0. Такой процесс на­зывается изохорным, для него

,

т. е. количество теплоты, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.

3. dU=0 – внутренняя энергия системы не изменяется и

,

т.е. сообщаемая системе теплота пре­вращается в эквивалентную ей внешнюю работу.

Для системы, содержащей 1 кг рабо­чего тела

. (2.9)

Проинтегрировав уравнения (2.8) и (2.9) для некоторого процесса, полу­чим выражение первого закона термоди­намики в интегральной форме:

; .

ЛЕКЦИЯ 3

Внутренняя энергия

Внутренняя энергия системы включа­ет в себя:

кинетическую энергию поступатель­ного, вращательного и колебательного движения частиц;

потенциальную энергию взаимодей­ствия частиц;

энергию электронных оболочек атомов;

внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в даль­нейшем под внутренней энер­гией будем понимать энергию хаотиче­ского движения молекул и атомов, вклю­чающую энергию поступательного, вра­щательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул явля­ется функцией температуры, значение потенциальной энергии зависит от сред­него расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. По­этому внутренняя энергия U есть функ­ция состояния тела.

Для сложной системы она определя­ется суммой энергий отдельных частей, т. е. обладает свойством аддитивности. Величина и=U/М, называемая удельной внутренней энер­гией (Дж/кг), представляет собой внутреннюю энергию единицы массы ве­щества.

В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она мо­жет быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

; ; .

Ее изменение в термодинамическом процессе не зависит от характера процесса и определяется только началь­ным и конечным состояниями тела:

;

— значение внутренней энергии в начальном состоянии, а — в конечном. Математически это означает, что бесконечно малое измене­ние внутренней энергии du есть полный дифференциал и; если выразить внутрен­нюю энергию в виде функции удельного объема и температуры, то

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодей­ствия между молекулами, не зависит от объема газа или давления , а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

Для задач технической термодинами­ки важно не абсолютное значение внут­ренней энергии, а ее изменение в различ­ных термодинамических процессах. По­этому начало отсчета внутренней энер­гии может быть выбрано произвольно. Например, в соответствии с международ­ным соглашением для воды за нуль при­нимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при 0 °С вне зависимости от давления.

 

Работа расширения

Работа в термодинамике, так же как и в механике, определяется произведени­ем действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ массой М и объемом V, заключенный в эластичную оболочку с поверхностью F.

 

Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой. Газ дей­ствует на каждый элемент оболочки dF с силой, равной pdF и, перемещая ее по нормали к поверхности на расстояние dn, совершает элементарную работу pdFdn. Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки: .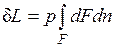

Из рисунка видно, что изменение объема dV выражается в виде интеграла по поверхности: 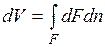, следовательно

. (3.1)

При конечном изменении объема работа против сил внешнего давления, называе­мая работой расширения, равна

Из (3.1) следует, что и dV всегда имеют одинаковые знаки:

если dV>0, то и >0, т. е. при расширении работа тела положительна, при этом тело само совершает работу;

если же dV<0, то и <0, т. е. при сжатии работа тела отрицательна: это означает, что не тело совершает работу, а на его сжатие затрачивается работа извне. Единицей измерения работы в СИ яв­ляется джоуль (Дж).

Отнеся работу расширения к 1 кг массы рабочего тела, получим

l = L/M; .

Величина, представляющая собой удельную работу, совершаемую систе­мой, содержащей 1 кг газа, равна

. (3.2)

Поскольку в общем случае р — вели­чина переменная, то интегрирование воз­можно лишь тогда, когда известен закон изменения давления р = р(v).

Формулы (3.1) — (3.2) справедливы только для равновесных процессов, при которых давление рабочего тела равно давлению окружающей среды.

В термодинамике для исследования равновесных процессов широко исполь­зуют р,v – диаграмму, в которой осью аб­сцисс служит удельный объем, а осью ординат — давление. Поскольку состоя­ние термодинамической системы опреде­ляется двумя параметрами, то на р,v – диаграмме оно изображается точкой. На рисунке точка 1 соответствует начально­му состоянию системы, точка 2 — конеч­ному, а линия 12 — процессу расшире­ния рабочего тела от v1 до v2. При бесконечно малом изменении объема площадь заштрихованной вертикальной полоски равна 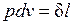; следовательно, работа процесса 12 изо­бражается площадью, ограниченной кри­вой процесса, осью абсцисс и крайними ординатами.

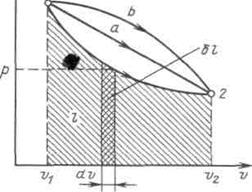
Таким образом, работа из­менения объема эквивалентна площади под кривой процесса в диаграмме р, v (рисунок 3.1).

Рисунок 3.1 - Графическое изображение работы в р, v – координатах

 

Каждому пути перехода системы из состояния / в состояние 2 (например, 12, 1а2 или 1b2) соответствует своя работа расширения.Следова­тельно, работа зависит от характера термодинамического процесса, а не явля­ется функцией только исходного и ко­нечного состояний системы. С другой стороны, зависит от пути интегри­рования и, следовательно, элементарная работа 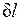не является полным диффе­ренциалом.

Работа всегда связана с перемеще­нием макроскопических тел в простран­стве, например перемещением поршня, деформацией оболочки, поэтому она ха­рактеризует упорядоченную (макрофизическую) форму передачи энергии от од­ного тела к другому и является мерой переданной энергии. Поскольку величина 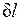пропорцио­нальна увеличению объема, то в качестве рабочих тел, предназначенных для пре­образования тепловой энергии в механи­ческую, целесообразно выбирать такие, которые обладают способностью значи­тельно увеличивать свой объем. Этим качеством обладают газы и пары жидко­стей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внут­реннего сгорания — газообразные про­дукты сгорания того или иного топлива.

 

Теплота

Помимо макрофизической формы пе­редачи энергии — работы существует также и микрофизическая, т. е. осуще­ствляемая на молекулярном уровне фор­ма обмена энергией между системой и окружающей средой. В этом случае энергия может быть передана системе без совершения работы. Мерой количест­ва энергии, переданной микрофизиче­ским путем, служит теплота.

Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвек­цией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности температур между телами.

Как будет показано ниже, элементар­ное количество теплоты , так же как и L, не является полным дифференциа­лом в отличие от дифференциала внут­ренней энергии dU. За этой математиче­ской символикой скрыт глубокий физиче­ский смысл различия понятий внутрен­ней энергии, теплоты и работы.

Внутренняя энергия — это свойство самой системы, она характеризует состо­яние системы. Теплота и работа — это энергетические характеристики процес­сов механического и теплового взаи­модействий системы с окружающей средой. Они характеризуют те количест­ва энергии, которые переданы системе или отданы ею через ее границы в опре­деленном процессе.

Энтальпия

В термодинамике важную роль игра­ет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

.

Так как входящие в нее величины явля­ются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, ра­бота и теплота, она измеряется в джоу­лях (Дж).

Энтальпия обладает свойством адди­тивности. Величина

,

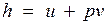называемая удельной энталь­пией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг ве­щества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представ­лена в виде функции двух любых пара­метров состояния:

; ; ,

а величина dh является полным диффе­ренциалом.

Изменение энтальпии в любом про­цессе определяется только начальным и конечным состояниями тела и не за­висит от характера процесса.

Физический смысл энтальпии выяс­ним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G.

Энергия этой системы складывается из внутренней энергии га­за и потенциальной энергии поршня с грузом в поле внешних сил: . В условиях равновесия (G = pF) эту функцию можно выразить через па­раметры газа: . Получаем, что , т.е. энтальпию можно трактовать как энергию расши­ренной системы.

Уравнение в случае, когда единственным видом ра­боты является работа расширения, с уче­том очевидного соотношения может быть записано в виде , или

.

Из этого соотношения следует, что если давление системы сохраняется неизменным, т. е. осуществляется изобар­ный процесс (dp=0), то

и .

т. е. теплота, подведенная к системе при постоянном давлении, идет только на из­менение энтальпии данной системы.

Это выражение очень часто исполь­зуется в расчетах, так как огромное ко­личество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбин и ре­активных двигателей, теплообменных ап­паратах), а также целый ряд процессов химической технологии и многих других осуществляется при постоянном давле­нии. Кстати, по этой причине в таблицах термодинамических свойств обычно при­водятся значения энтальпии, а не внут­ренней энергии.

Для идеального газа с учетом получим

Так как между энтальпией и внутрен­ней энергией существует связь 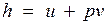, выбор начала отсчета одной из них не произволен: в точке, принятой за начало отсчета внутренней энергии, h = pv.

На­пример, для воды при t= 0.01ºC и р = 610,8 Па, u = 0, a

h = pv = 0,611 Дж/кг.

При расчетах практический интерес представляет изменение энтальпии в ко­нечном процессе: .

Энтропия

Как уже указывалось, величина не является полным диффе­ренциалом. Действительно, для того что­бы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который соверша­ет газ.

В математике доказывается, что диф­ференциальный двучлен всегда можно превратить в полный дифференциал пу­тем умножения (или деления) на интег­рирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты q является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновес­ных процессах:

. (3.3)

Выражение при равновесном изменении состояния газа есть полный дифференциал некоторой функции состо­яния. Она называется энтропией, обозначается для 1 кг газа через s и из­меряется в Дж/(кгК). Для произволь­ного количества газа энтропия, обозна­чаемая через S, равна S=Ms и измеря­ется в Дж/К.

Таким образом, аналитически энтро­пия определяется следующим образом:

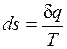. (3.4)

Формула (3.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции со­стояния энтропия может быть представ­лена в виде функции любых двух пара­метров состояния:

; ; .

 

Значение энтропии для заданного со­стояния определяется интегрированием уравнения (3.4):

где 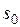— константа интегрирования.

При температурах, близких к абсо­лютному нулю, все известные вещества находятся в конденсированном состоя­нии. В. Нернст (1906 г.) эксперименталь­но установил, а М. Планк (1912 г.) окон­чательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристалличе­ской структурой, стремится к нулю, т. е. s₀ = 0 при Т = 0 К. Этот закон на­зывают третьим законом термодинамики или тепловой тео­ремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от про­извольного уровня.

Однако в технической термодинамике обычно используется не абсолютное зна­чение энтропии, а ее изменение в каком-либо процессе:

,

поэтому энтропию тоже часто отсчитыва­ют от произвольно выбранного уровня.

Получим формулы, позволяющие вы­числить изменение энтропии идеального газа. Для этого проинтегрируем уравне­ние (3.3), положив для простоты cv = const:

. (3.5)

Из уравнения Клапейрона, записан­ного для состояний 1 и 2, следует:

.

После подстановки отношений и в выражение (3.4) получим следующие формулы для изменения энтро­пии идеального газа:

;

. (3.6)

Поскольку энтропия есть функция со­стояния рабочего тела, уравнениями (3.5) — (3.6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

Рисунок 3.2 - Графическое изображение теплоты в T, s – координатах

 

Понятие энтропии позволяет ввести чрезвычайно удобную для термодинами­ческих расчетов Т, s-диаграмму, на кото­рой (как и на p,v -диаграмме) состояние термодинамической системы изобража­ется точкой, а равновесный термодина­мический процесс линией (Рисунок 3.2).

В равновесном процессе

;

.

Очевидно, что в Т, s-диаграмме эле­ментарная теплота процесса изобра­жается элементарной площадкой с высо­той Т и основанием ds, а площадь, огра­ниченная линией процесса, крайними ординатами и осью абсцисс, эквивалент­на теплоте процесса.

Формула показывает, что ds и имеют одинаковые знаки, следова­тельно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу ( >0 ) его энтропия возрастает (ds>0), а при отводе теплоты ( <0) — убывает (ds<0).

ЛЕКЦИЯ 4