Детерминированные процессы.
Периодические представимы как X(t)=X(t+T) и разлагаются в ряд Фурье X(t) = 


с соизмеримыми частотами  (отношение
(отношение  является рациональным числом).
является рациональным числом).


Например, радиосигнал с определённой частотой.
Приближённо такими процессами являются: напряжение на выходе электрического генератора; вибрация двигателя внутреннего сгорания.
Если в спектре присутствуют частоты, отношения которых  является иррациональным числом, то процесс называется квазипериодическим. К таким процессам относится вибрация многомоторного самолета, в котором двигатели не синхронизированы.
является иррациональным числом, то процесс называется квазипериодическим. К таким процессам относится вибрация многомоторного самолета, в котором двигатели не синхронизированы.
Все остальные процессы считаются переходными (система не вышла на установившийся режим)
Примеры.
Температура воды в чайнике после отключения питания:

Затухание маятника после толчка:

Напряжение в тросе, который разрывается:

Случайные процессы
Теорией случайных процессов ( CП) называется математическая наука, изучающая случайные явления в динамике их развития.
Определение СП [1,3]
Случайные процессы являются матмоделями для описания случайных явлений, развивающихся во времени. При этом предполагается, что состояние в текущий момент времени есть случайная величина  Пространство элементарных событий
Пространство элементарных событий  предполагается измеримым (т.е. на нём определена
предполагается измеримым (т.е. на нём определена  -алгебра его подмножеств
-алгебра его подмножеств  . Предполагается, что на измеримом пространстве
. Предполагается, что на измеримом пространстве 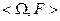 задана вероятностная мера Р, то есть для любого события
задана вероятностная мера Р, то есть для любого события  определена его вероятность Р(А). Таким образом задано вероятностное пространство
определена его вероятность Р(А). Таким образом задано вероятностное пространство 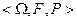 )
)
Случайный процесс есть семейство случайных величин (СВ)  , определённых на
, определённых на 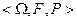 , где под параметром t понимается время и
, где под параметром t понимается время и  .
.
Пусть  - фиксированный момент. Случайная величина
- фиксированный момент. Случайная величина 
 называется сечением случайного процесса в точке
называется сечением случайного процесса в точке  .
.
СП можно рассматривать как совокупность случайных величин, зависящих от параметра t. Процесс может быть действительным или комплексным в зависимости от вида СВ 
Мы фиксировали время. А теперь пусть  - фиксируемый результат испытания. Тогда неслучайная функция
- фиксируемый результат испытания. Тогда неслучайная функция  (в которую превращается процесс в результате испытания) называется реализацией (траекторией, выборочной функцией) СП. С реализациями мы чаще всего имеем дело на практике. Таким образом, СП можно рассматривать как совокупность всех возможных его реализаций.
(в которую превращается процесс в результате испытания) называется реализацией (траекторией, выборочной функцией) СП. С реализациями мы чаще всего имеем дело на практике. Таким образом, СП можно рассматривать как совокупность всех возможных его реализаций.

СП классифицируют в зависимости от непрерывности или дискретности  и Т:
и Т:
1) СП называется процессом с дискретным временем (или случайной последовательностью) если система, в которой он протекает, может менять своё состояние в дискретные моменты времени.
Например: некто накупил всяких лотерейных билетов. Выигрыши происходят в определённые дни. Случайный процесс  - число билетов, выигравших до момента времени t.
- число билетов, выигравших до момента времени t.
2) СП называется процессом с непрерывным временем, если переходы системы могут происходить в любой момент 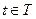 .
.
Например: техническое устройство может иметь три состояния: работает нормально, работает с перебоями, ремонтируется. Случайный процесс  - состояние устройства в момент времени t.
- состояние устройства в момент времени t.
3) СП называется процессом с дискретными состояниями, если в любой момент времени множество его состояний конечно или счётно (если любое его сечение – дискретная СВ).
4) СП называется процессом с непрерывными состояниями, если множество его состояний несчётно (если любое его сечение – непрерывная или смешанная СВ)..
Законы распределения СП [1,2]
Универсальной, исчерпывающей характеристикой СВ является её функция распределения  .
.
Пусть мы имеем СП. При любом фиксированном t получим сечение. Это СВ, которая имеет закон распределения.  - одномерный закон распределения. Функция зависит от двух аргументов
- одномерный закон распределения. Функция зависит от двух аргументов 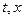 . Является ли
. Является ли  исчерпывающей характеристикой? Нет, так как характеризует свойства одного отдельного сечения.
исчерпывающей характеристикой? Нет, так как характеризует свойства одного отдельного сечения.

Двумерный закон распределения 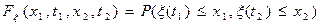 -
-
функция 4-х аргументов. Это уже неприятно. Далее – трехмерные и т.д. Теоретически число сечений можно увеличивать неограниченно.
Однако на практике очень часто вполне можно ограничиться двумерным законом. Например, огромный класс марковских процессов (процессы без последствия), гауссовские процессы (очень широкий класс процессов, которые являются моделями сигналов и помех в радиотехнике), для которых двумерный закон распределения является исчерпывающей характеристикой.
В общем случае мы имеем n сечений:
Пусть  - действительный СП и задано некоторое произвольное множество моментов времени. Соответствующая совокупность случайных величин
- действительный СП и задано некоторое произвольное множество моментов времени. Соответствующая совокупность случайных величин  имеет n – мерную функцию распределения
имеет n – мерную функцию распределения
 .
.
Сем ейство конечномерных распределений СП – это совокупность n-мерных функций распределения для различных n и моментов t.
Если  допускает представление
допускает представление
 ,
,
где  - некоторая измеримая по Лебегу неотрицательная функция, такая что
- некоторая измеримая по Лебегу неотрицательная функция, такая что  , то
, то  имеет n- мерную плотность распределения
имеет n- мерную плотность распределения  .
.
Семейство конечномерных распределений является основной характеристикой СП, полностью определяющей его свойства. Говорят, что СП задан, если задано его семейство конечномерных распределений.
Свойства функции распределения.
1)  (условие нормировки);
(условие нормировки);
2)  непрерывны справа по переменным
непрерывны справа по переменным  ;
;
3) Если какая либо переменная  ,то
,то  ,
,
Если все  , то
, то 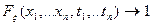 ;
;
4) Функция  монотонна по каждому аргументу
монотонна по каждому аргументу  ;
;
5) Для любой перестановки  индексов
индексов 
 ;
;
6) 
 и
и 
 .
.
Cвойства 5 и 6 – условия согласованности семейства конечномерных распределений.
Основополагающий результат теории СП –
Теорема Колмогорова.
Пусть задано некоторое семейство конечномерных функций распределения
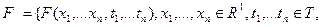
 ,
,






