Задача 1. Найти расстояние от точки M0 (1,3,5) до плоскости 
.
Решение. По формуле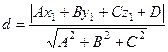 
получаем, что
= 
= 
.
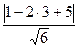Ответ.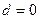 
.
Задача 1а. Найти расстояние от точки M0 (7,15,22) до плоскости .
Решение. По формуле 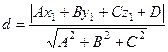получаем, что
= 
= 
.
Ответ.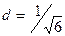 
.
Задача 2. (На плоскости). Даны три точки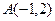 
, 
, 
.
Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С до этой прямой (то есть высоту треугольника АВС).
Решение. Вектор АВ равен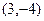 
, и это есть направляющий на прямой, порождаемой отрезком АВ. Можем считать, что он отложен от точки А. В то же время вектор АМ до произвольной точки 
, который равен 
, пропорционален АВ. Тогда 
, то есть 
, и уравнение прямой: 
.
Теперь по формуле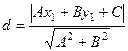 
найдём расстояние от этой прямой до точки . 
= 
= 
.
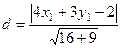Ответ. Прямая , расстояние 3.
Задача 3. Найти угол между двумя плоскостями: 
и 
.
Решение. Нормали к этим плоскостям: 
и 
.
= 
= 
.
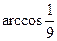Ответ. 
, что приблизительно составляет 83,6 градусов.
Прямая в пространстве
Задача 4. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке 
и направляющему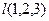 
.
Решение. Если отложить вектор от к произвольной точке 
, то вектор 
коллинеарен вектору 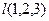, то есть их координаты пропорциональны. Тогда:
(это мы сейчас получили канонические уравнения).
Если каждую такую дробь приравнять к некоторому параметру 
, то
, 
, 
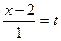, следовательно:
, 
, 
.
Тогда 
- параметрические уравнения.
Ответ. ,
Задача 5. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке и направляющему (с произвольными случайно взятыми параметтрами, которые придумает группа).
Задача 6. Построить уравнение прямой, лежащей в пересечении двух плоскостей 
и 
.
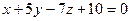Решение. Векторное произведение нормалей 
это направляющий вектор, вычислим его. 
=
= 
.
Итак, направляющий вектор 
.
Теперь нужно найти хотя бы одну точку на этой прямой. Чтобы взять произвольную точку из пересечения плоскостей, можно положить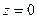 
и решить систему, вычислив 
.
Два уравнения, без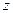 
, приводят к такой системе: 
.
Выразим из 2-го 
и подставим в 1-е.
Получим 
. Тогда 
, т.е. 
.
Но тогда 
. Итак, получили точку 
.
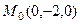Вектор от этой точки к произвольной точке 
равен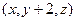 
и он попорционален направляющему вектору. Тогда
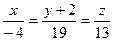канонические уравнения этой прямой.
Приравнивая все эти дроби к , можно вычислить и параметрические уравнения 
.
Ответ. , .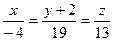
Задача 7. Доказать, что прямая 
пересекает ось 
и найти точку пересечения.
Решение. Если прямая пересекает ось , то точка пересечения имеет вид 
. Если в первые две дроби вместо подставить 0, то получим 
. Тогда 
, т.е. 
.
Ответ. (0,0,1).
Задача 8. Найти угол между прямой 
и плоскостью 
.
Решение. Формула, выведенная в лекциях: 
.
Направляющий к прямой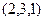 
, нормаль к плоскости 
.
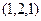Их скалярное произведение равно 9.
Модули векторов равны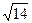 
и 
.
Ответ. 
.
Задача 9. Найти параметрические и канонические уравнения прямой, перпендикулярной к плоскости треугольника с вершинами 
, 
, 
и проходящей через вершину А.
Решение. Направляющие АВ и АС это (3,3,0) и 
.
Их векторное произведение:
= 
= 
.
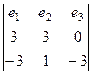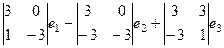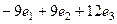Итак, вектор 
. Но можно в том же направлении выбрать вектор короче в 3 раза (для удобства вычислений) ведь направление от этого не изменится. Итак, пусть направляющий для прямой 
, точка . Вектор от к произвольной точке имеет вид
. Он коллинеарен , есть пропорциональность координат. Тогда 
. Это и есть канонические уравнения. Перейти к параметрическим можно так же, как и в прошлых задачах: приравнять все дроби к и выразить всё через .
Ответ. Канонические ,
параметрические 
.
Задача 10. Доказать, что две прямые в пространстве
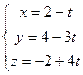и 
пересекаются, и найти точку пересечения.
Решение. Если у них естьь общая точка, то можно приравнять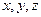 
из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах 
, а во вторых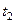 
.
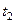перенесём все , в одну сторону, а константы в другую, чтобы система была записана в стандартной форме.
расширенная матрица: 
Преобразуем методом Гаусса. От 2-й строки отнимем утроенную 1-ю, а к 3-й прибавим 4-кратную 1-ю.
т.е.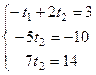 
то есть сразу же 
из 2-го и 3-го уравнений, и они не противоречат друг другу. Кстати, эта система совместна, равнги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем 
, т.е.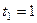 
.
Затем подставить 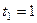в первые уравнения либо во вторые,
получим одни и те же значения для .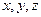
, т.к. 
и 
Ответ точка пересечения (1,1,2).
Задача 11. Доказать, что две прямые в пространстве:
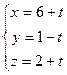и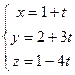 
скрещивающиеся, и найти расстояние между ними.
Решение. Решая систему уравнений, как в прошлой задаче, здесь мы обнаружим, что система несовместна.
матрица: 
прибавим ко 2-й строке 1-ю, а от 3-й отнимем 1-ю.
получили систему 
2-е и 3-е уравнения противоречат друг другу. Система не имеет решений, значит, эти 2 прямые не имеют ни одной общей точки.
Так как направляющие векторы 
и 
не коллинеарны, то прямые не параллельные, а скрещивающиеся.
Найдём расстояние между ними. Точку на каждой прямой можно найти, присваивая 
. 
, 
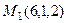. Вектор, соединяющий две прямых, 
.
Вычисляем по формуле 
.
Смешанное произведение с помощью определителя.
= 
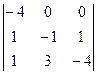(прибавили 2-ю строку к 1-й)
= 
= 
, а по модулю получается 4.
= 
= 
.
Модуль векторного произведения равен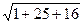 
= 
.
= 
. Ответ. .
Дом. задача 1. (12.22 [1]) Доказать, что прямые
и 
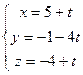пересекаются и найти точку.
Ответ. (3,7,-6).
Дом. задача 2. (12.35 [1])
Вычислить расстояние между скрещивающимися прямым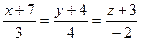и:
и 
Ответ 13.
Практика 13. Прямая в пространстве. Кривые и поверхности.
Практика 14. Повторение и контрольная работа.
Темы 2-й контрольной:
5. Векторная алгебра (скалярные, векторные произведения).
6. Системы уравнений, метод Гаусса
7. Собственные числа и векторы
8. Уравнения прямой и плоскости
Приложение 1.
Пример одного варианта контрольных работ.
Темы 1-й контрольной:
1. Действия над матрицами.
2. Определители.
3. Обратная матрица.
4. Ранг матрицы.
Вариант:
1) Умножить матрицы 
2) Найти определитель 
3) Найти обр.матрицу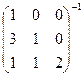 
4) Найти ранг матрицы 
Темы 2-й контрольной:
5. Векторная алгебра (скалярные, векторные произведения).
6. Системы уравнений, метод Гаусса
7. Собственные числа и векторы
8. Уравнения прямой и плоскости
Вариант:
5) Векторы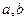 
выражены через 
: 
, 
.
, 
, угол между ними 60 градусов. Найти 
.
6) Решить систему 
7) Найти собственные числа и собственные векторы линейного оператора, заданного матрицей 
.
8) Найти уравнение плоскости, проходящей через точку (1,4,2) перпендикулярно вектору (2,1,2).
Литература.
[1]. Магазинников Л.И. Практикум по линейной алгебре и аналитической геометрии.
[2]. Демидович Б.П. Сборник задач и упражнений по математическому анализу.
