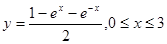Семестр.
Рекомендованная литература.
а) Основная литература
1.Баврин И.И., Матросов В.Л. Общий курс высшей математики: Учеб. для студентов физ.-мат. спец. пед.вузов. – М.: Просвещение, 2008.
2.Бермант, А.Ф. Краткий курс математического анализа [Текст]: учебник для инж.-техн. и гуман. спец. вузов / А.Ф. Бермант, И.Г. Араманович. - 13-е изд., стереотип. - СПб.:Лань, 2006. - 736 с.:ил.- (Серия "Лучшие классические учебники")
3.Бугров, Я.С. Высшая математика. В 3 т. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного [Текст]: учебник для вузов по инж.-техн. спец. / Я.С. Бугров, С.М. Никольский;под ред. В.А. Садовничего. - 7-е изд., стереотип. - М.:Дрофа, 2005. - 511 с. - (Высшее образование: Современный учебник
4..Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и задачах. – М., 2008, 2009.
5.Общий курс высшей математики для экономистов. [Текст]:колл авторов под ред. В.И. Ермакова.-М.:ИНФРА-М., 2010.-656с.
6..Дюженкова, Л.И. Практикум по высшей математике. В 2 ч. Ч.1. [Текст]:ЛИ. Дюженкова., О.О. Дюженкова, Г.А. Михалин. Пер с укр.-М.: БИНОМ. Лаборатория знаний, 2011-448с.
7.Дюженкова, Л.И. Практикум по высшей математике. В 2 ч. Ч.2. [Текст]:ЛИ. Дюженкова., О.О. Дюженкова, Г.А. Михалин. Пер с укр.-М.: БИНОМ. Лаборатория знаний, 2011-468с.
8..Краснов М.Л., Киселев А.И. и др. Вся высшая математика (в пяти частях). – М. Эдиториал УР СС, 2003.
б) Дополнительная литература
9..Берман Г.Н. Сборник задач по курсу математического анализа. - Наука, 2001.
10..Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М., 1997.
11.Минорский В.П. Сборник задач по высшей математике. - М., 2000.
12.Кремер Н.Ш. и др. Высшая математика для экономистов. – М.: ЮНИТИ-ДАНА, 2007.
13.Кремер Н.Ш. и др. Высшая математика для экономистов: практикум. – М.: ЮНИТИ-ДАНА, 2007.
14.Малугин В.А. Математика для экономистов: математический анализ. Задачи и упражнения. – М.: ЭксМО, 2006.
в) Электронные ресурсы
15.Балдин К.В. Краткий курс высшей математики [Электронный ресурс]: учебник/ Балдин К.В., Балдин Ф.К., Джеффаль В.И.— Электрон. текстовые данные.— М.: Дашков и К, 2013.— 512 c.— Режим доступа: http://www.iprbookshop.ru/14611.— ЭБС «IPRbooks», по паролю
16.Бесов О.В. Лекции по математическому анализу [Электронный ресурс]/ Бесов О.В.— Электрон. текстовые данные.— М.: ФИЗМАТЛИТ, 2014.— 476 c.— Режим доступа: http://www.iprbookshop.ru/24291.— ЭБС «IPRbooks», по паролю
Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
| № варианта | № варианта | ||
| 1.1 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.16 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.2 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.17 | 1)  ;
2) ;
2)  ;
3) ;
3) 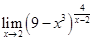 . .
|
| 1.3 | 1) 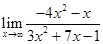 ;
2) ;
2)  ;
3) ;
3)  . .
| 1.18 | 1) 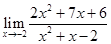 ;
2) ;
2)  ;
3) ;
3) 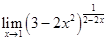 . .
|
| 1.4 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.19 | 1)  ;
2) ;
2) 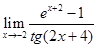 ;
3) ;
3) 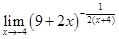 . .
|
| 1.5 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.20 | 1)  ;
2) ;
2) 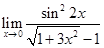 ;
3) ;
3) 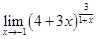 . .
|
| 1.6 | 1)  ;
2) ;
2)  ;
3) ;
3) 
| 1.21 | 1) 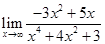 ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.7 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.22 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.8 | 1) 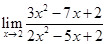 ;
2) ;
2)  ;
3) ;
3)  . .
| 1.23 | 1) 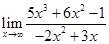 ;
2) ;
2) 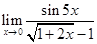 ;
3) ;
3)  . .
|
| 1.9 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.24 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.10 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.25 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.11 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.26 | 1)  ;
2) ;
2)  ;
3) ;
3) 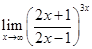 . .
|
| 1.12 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.27 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.13 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.28 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.14 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 1.29 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 1.15 | 1)  ;
2) ;
2) 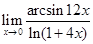 ;
3) ;
3)  . .
| 1.30 | 1) 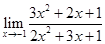 ;
2) ;
2)  ;
3) ;
3)  . .
|
Найти производную 1-го порядка данных функций.
| 2.1 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.16 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.2. | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.17 | 1)  ;
2) ;
2)  3)
3) 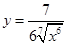 . .
|
| 2.3. | 1) 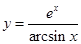 ;
2) ;
2)  ;
3) ;
3)  . .
| 2.18 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.4. | 1)  ;
2) ;
2)  ;
3) ;
3) 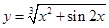 . .
| 2.19 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.5. | 1) 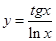 ;
2) ;
2)  ;
3) ;
3)  . .
| 2.20 | 1)  ;
2) ;
2) 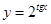 3)
3)  . .
|
| 2.6. | 1)  ;
2) ;
2)  ;
3) ;
3) 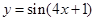 . .
| 2.21 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.7. | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.22. | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.8. | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.23 | 1) 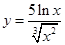 ;
2) ;
2)  3)
3)  . .
|
| 2.9. | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.24 | 1) 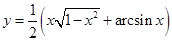 ;
2) ;
2)  3)
3)  . .
|
| 2.10 | 1)  ;
2) ;
2)  ;
3) ;
3) 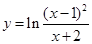 . .
| 2.25 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.11 | 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 2.26 | 1)  ;
2) ;
2)  3)
3)  . .
|
| 2.12 | 1)  ;
2) ;
2)  ;
3) ;
3) 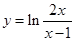 . .
| 2.27 | 1)  ;
2) ;
2)  3)
3) 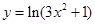 . .
|
| 2.13 | 1)  ;
2) ;
2)  3)
3)  . .
| 2.28 | 1)  ;
2) ;
2) 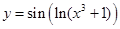 ;
3) ;
3)  . .
|
| 2.14 | 1)  ;
2) ;
2) 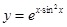 ;
3) ;
3)  . .
| 2.29 | 1) 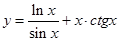 ;
2) ;
2) 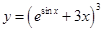 ;
3) ;
3) 
|
| 2.15 | 1)  ;
2) ;
2)  3)
3)  . .
| 2.30 | 1)  ;
2) ;
2)  ;
3) ;
3) 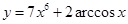 . .
|
3. Составить уравнение касательной и нормали к графику кривой у = f (x) в точке с абсциссой х 0.
| 3.1 |  , х 0 = − 1 , х 0 = − 1
| 3.16 | 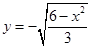 , х 0 = , х 0 = 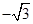
|
| 3.2 |  , х 0 = − 1 , х 0 = − 1
| 3.17 |  , х 0 = 1 , х 0 = 1
|
| 3.3. |  , х 0 = 1 , х 0 = 1
| 3.18 |  , х 0 = 1 , х 0 = 1
|
| 3.4 | 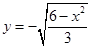 , х 0 = , х 0 = 
| 3.19 |  , х 0 = 1 , х 0 = 1
|
| 3.5 |  , х 0 = 2 , х 0 = 2
| 3.20 |  , х 0 = − , х 0 = − 
|
| 3.6 |  , х 0 = 1 , х 0 = 1
| 3.21 |  , х 0 = 4 , х 0 = 4
|
| 3.7 |  , х 0 = 1 , х 0 = 1
| 3.22 | 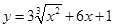 , х 0 = 1 , х 0 = 1
|
| 3.8 |  , х 0 = 1 , х 0 = 1
| 3.23 |  , х 0 = 0 , х 0 = 0
|
| 3.9 | 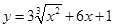 , х 0 = − 1 , х 0 = − 1
| 3.24 |  , х 0 = − 1 , х 0 = − 1
|
| 3.10 | 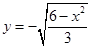 , х 0 = − , х 0 = − 
| 3.25 |  , х 0 = , х 0 = 
|
| 3.11 |  , х 0 = 1 , х 0 = 1
| 3.26 |  , х 0 = , х 0 = 
|
| 3.12 |  , х 0 = 1 , х 0 = 1
| 3.27 |  , х 0 = − 1 , х 0 = − 1
|
| 3.13 |  , х 0 = − 1 , х 0 = − 1
| 3.28 |  , х 0 = − 2 , х 0 = − 2
|
| 3.14 | 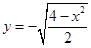 , х 0 = , х 0 = 
| 3.29 |  , х 0 = 1 , х 0 = 1
|
| 3.15 |  , х 0 = 1 , х 0 = 1
| 3.30 |  , х 0 = , х 0 = 
|
4. Исследовать функцию по полной схеме и построить график. Исследование функции рекомендуется провести по схеме:
1) найти область определения функции;
2) исследовать функцию на непрерывность, найти асимптоты графика функции или показать, что их нет;
3) найти точки пересечения графика с осями координат;
4) проверить функцию на четность и нечетность, сделать вывод о симметричности графика функции;
5) найти интервалы возрастания и убывания функции, экстремумы функции;
6) найти интервалы выпуклости и вогнутости графика функции, точки перегиба.
| 4.1 | 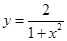
| 4.16 | 
|
| 4.2 | 
| 4.17 | 
|
| 4.3 | 
| 4.18 | 
|
| 4.4. | 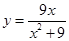
| 4.19 | 
|
| 4.5 | 
| 4.20 | 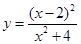
|
| 4.6 | 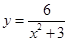
| 4.21 | 
|
| 4.7 | 
| 4.22 | 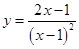
|
| 4.8 | 
| 4.23 | 
|
| 4.9 | 
| 4.24 | 
|
| 4.10 | 
| 4.25 | 
|
| 4.11 | 
| 4.26 | 
|
| 4.12 | 
| 4.27 | 
|
| 4.13 | 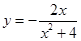
| 4.28 | 
|
| 4.14 | 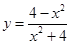
| 4.29 | 
|
| 4.15 | 
| 4.30 | 
|
Задача 5 Найти неопределенные интегралы.
5.1. 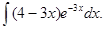
5.2. 
5.3. 
5.4. 
5.5. 
5.6. 
5.7. 
5.8. 
5.9. 
5.10. 
5.11. 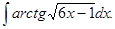
5.12. 
5.13. 
5.14. 
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 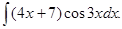
5.21. 
5.22. 
5.23. 
5.24. 
5.25. 
5.26. 
5.27. 
5.28. 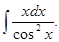
5.29. 
5.30. 
5.31. 
Задача 6. Найти неопределенные интегралы.
6.1. 
6.2. 
6.3. 
6.4. 
6.5. 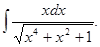
6.6. 
6.7. 
6.8. 
6.9. 
6.10. 
6.11. 
6.12. 
6.13. 
6.14. 
6.15. 
6.16. 
6.17. 
6.18. 
6.19. 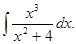
20. 
6.21. 
6.22. 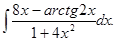
6.23. 
6.24. 
6.25. 
6.26. 
6.27. 
6. 28. 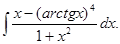
6.29. 
6.30. 
6.31. 
Задача 7 Найти неопределенные интегралы.
7.1. 
7.2. 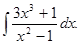
7.3. 
7.4. 
7.5. 
7.6. 
7.7. 
7.8. 
7.9. 
7.10. 
7.11. 
7.12. 
7.13. 
7.14. 
7.15. 
7.16. 
7.17. 
7.18. 
7.19. 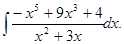
7.20. 
7.21. 
7.22. 
7.23. 
7.24. 
7.25. 
7.26. 
7.27. 
7.28. 
7.29. 
7.30. 
7.31. 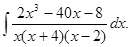
Задача 8 Найти неопределенные интегралы.
8.1. 
8.2. 
8.3. 
8.4. 
8.5. 
8.6. 
8.7. 
8.8. 
8.9. 
8.10. 
8.11. 
8.12. 
8.13. 
8.14. 
8.15. 
8.16. 
8.17. 
8.18. 
8.19. 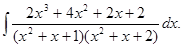
8.20. 
8.21. 
8.22. 
8.23. 
8.24. 
8.25. 
8.26. 
8.27. 
8.28. 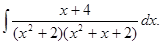
8.29. 
8. 30. 
8. 31. 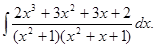
Задача 9. Вычислить определенные интегралы.
9.1. 
9.2. 
9.3. 
9.4. 
9.5. 
9.6. 
9.7. 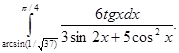
9.8. 
9.9. 
9.10. 
9.11. 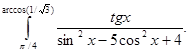
9.12. 
9.13. 
9.14. 
9.15. 
9.16. 
9.17. 
9.18. 
9.19. 
9.20. 
9.21. 
9.22. 
9.23. 
9.24. 
9.25. 
9.26. 
9.27. 
.9.28. 
9.29. 
9.30. 
9.31. 
Задача 10. Вычислить определенные интегралы.
10.1. 
10.2. 
10.3. 
10.4. 
10.5. 
10.6. 
10.7. 
10.8. 
10.9. 
10.10. 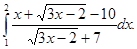
10.11. 
10.12. 
10.13. 
10.14. 
10.15. 
10.16. 
10.17. 
10.18. 
10.19. 
10.20. 
10.21. 
10.22. 
10.23. 
10. 24. 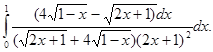
10.25. 
10.26. 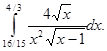
10.27. 
10.28. 
10.29. 
10.30. 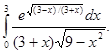
10.31. 
Задача 11. Вычислить площади фигур, ограниченных графиками функций.
11.1. 
11.2. 
11.3. 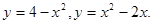
11.4. 
11.5.  11.6.
11.6. 
11.7. 
11.8. 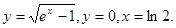
11.9. 
11.10. 
11.11. 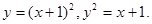
11.12. 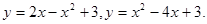
11.13. 
11.14. 
11.15. 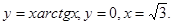
11.16. 
11.17. 
11.18. 
11.19. 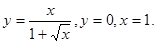
11.20. 
11.21. 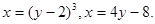
11.22. 
11.23. 
11.24. 
11.25. 
11.26. 
11.27. 
11.28. 
11.29. 
11.30. 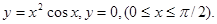
11.31. 
Задача 12. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
12.1. 
12.2. 
12.3. 
12.4. 
12.5. 
12.6. 
12.7. 
12.8. 
12.9. 
12.10. 
12.11. 
12.12. 
12.13. 
12.14. 
12.15. 
12.16. 
12.17. 
12.18. 
12.19. 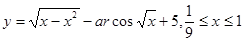
12.20. 
12.21. 
12.22. 
12.23. 
12.24. 
12.25. 
12.26. 
12.27. 
12.28. 
12.29. 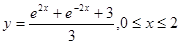
12.30. 
12.31.