Схема вычитающего счетчика на триггерах, переключающихся перепадом 1/0, приведена на рис. 4.3.3. По S-входам в разряды счетчика заносится двоичное число, из которого нужно вычесть число, представляемое количеством входных импульсов. При построении такого счетчика реализуется закономерность вычитания 1 из двоичного числа: первая 1, встретившаяся при просмотре этого числа справа налево, меняется на 0, а все предшествующие 0 меняются на 1. Например:
1002 – 0012 = 0112 (4 – 1 = 3); 0102 – 0012 = 0012 (2 – 1 = 1).
Поэтому счетный вход триггера, переключающегося перепадом 1/ 0, надо соединить не с прямым выходом предыдущего триггера (как в режиме суммирования), а с его инверсным выходом, на котором присутствует лог. 1, когда триггер находится в нулевом состоянии. Действительно, пусть счетчик имеет два разряда, в которые занесены 1 (число 3). При этом на инверсных выходах разрядов присутствуют лог. 0. Первый входной импульс переключает первый разряд счетчика в 0, и на его инверсном выходе возникает непереключающий перепад 0/1 – второй разряд остается в прежнем состоянии. Второй входной импульс вновь переключает первый разряд, и на его инверсном выходе появляется переключающий перепад 1/0, который устанавливает второй разряд в 0. Третий входной импульс опять переключает первый разряд, но теперь на его инверсном выходе формируется непереключающий перепад 0/1, поэтому второй разряд остается в нулевом состоянии. В результате три входных импульса обнуляют двухразрядный счетчик, осуществив вычитание из него числа 3 (0112). Следующий входной импульс, воздействуя на обнуленный счетчик, установит все его триггеры (как обычно, имеются в виду прямые выходы) в 1, так как при переключении каждого из них, начиная с первого, на инверсном выходе будет формироваться перепад 1/0, переключающий следующий разряд.
Структура реверсивного счетчика.
Реверсивный счетчик должен работать как на сложение, так и на вычитание. Из рассмотрения схем, представленных на рис. 4.3.1 и 4.3.3, следует, что в суммирующем счетчике каждый последующий триггер получает информацию с прямого выхода предыдущего, а в вычитающем – с инверсного выхода, т. е. для перехода от сложения к вычитанию и обратно надо изменять подключение счетного входа последующего триггера к выходу предыдущего.
Такая программа реализуется в схеме реверсивного счетчика, приведенной на рис. 4.3.4. Счетный вход каждого триггера через дизъюнктор может присоединяться к прямому выходу предыдущего триггера (через конъюнктор верхнего ряда) или к инверсному выходу (через конъюнктор нижнего ряда). Чтобы осуществить суммирование, на линию сложения со входа Р подается 1, которой вводятся в действие конъюнкторы верхнего ряда. При этом на шине вычитания присутствует 0, за счет чего конъюнкторы нижнего ряда выключены. Вычитание осуществляется при Р = 0, т. е. с подачей 1 на линию вычитания и 0 на шину сложения. Заносимое в счетчик число читается по выходам Q3, Q4, Q1.
Счетчики с последовательным переносом, имея простую структуру, обладают рядом недостатков. Один из них состоит в относительно низком быстродействии: к k -му разряду переключающий перепад проходит через (k — 1) предыдущих разрядов, поэтому интервал между соседними входными импульсами должен превышать t n (n – 1), где t n – время переключения триггера; n – число разрядов счетчика. Другим недостатком является то, что в ходе переключения младшие разряды счетчика принимают уже новые состояния, в то время как старшие еще находятся в прежнем, т. е. при смене одного числа другим счетчик проходит ряд промежуточных состояний, каждое из которых может быть принято фиксирующим устройством за окончательное.
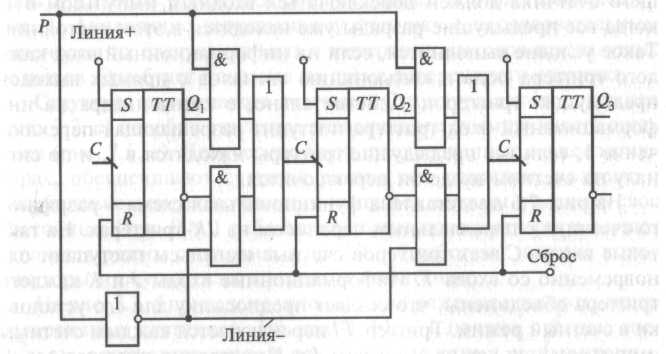
Рисунок 4.3.4.






