Тапсырма
1. Z0 = 0,4321 болсын Z1 мен Z2-ні орта шаршы алгоритмі бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
2. Z0 = 0,3437 мен Z1 = 0,6752 болсын Z2 мен Z3-ті орта көбейтінді алгоритм бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
3. Z0 = 1,5687 болсын Z1, Z2 мен Z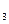 
-ні орта шаршы алгоритмі бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
4. Z0 = 2,9438 мен Z1 = 1,6834 болсын Z2, Z3 мен Z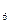 
-ті орта көбейтінді алгоритм бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
5. Z0 = 1,6502 болсын Z1, Z2,Z3 мен Z 
-ні орта шаршы алгоритмі бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
6. Z0 = 0,7862 мен Z1 = 0,1234 болсын Z2, Z3мен Z 
-ті орта көбейтінді алгоритм бойынша анықтаңыз. Алгоритмнің блок-схемасын құрыңыз.
Практикалық сабақты өткізу түрі: жеке жоба жасау
Әдістемелік ұсыныс:
Бақылау мысалы 1. Z0 = 0,5556 болсын. Орта шаршы алгоритмі көмегімен базалық тізбектің 3 жаңа нақтыламаларын алыңыз.
Шешуі. Z0 = 0,5556 болғандықтан, k = 2
Z0 = 0,5556, Z02 = 0,30869136,
Z1 = 0,8691, Z12 = 0,75533481,
Z2 = 0,5334, Z22 = 0,28451556,
Z3 = 0,4515, және т.с.с.
Бақылау мысалы 2. Z0 = 0,5556 мен Z1 = 0,8691 болсын. Орта көбейтінді алгоритмі көмегімен базалық тізбектің 2 жаңа нақтыламаларын алыңыз.
Шешуі.
Z0 = 0,5556, Z1 = 0,8691, Z0* Z1 = 0,48287196,
Z2 = 0,2871, Z1* Z2 = 0,24951861,
Z3 = 0,9518 және т.с.с
Ұсынылатын әдебиеттер: 1нег (8-17), 3нег (462-480), 6қос (10-25), 8қос (19-20)
Тақырып 1.2 Кездейсоқ сандарды модельдеудің конгруэнтті әдістері
Тапсырма
1. Шегерінділер әдісінің келесі параметрлері берілсін: а=401, с=201. Тізбек периоды Р=256 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 5 жаңа нақтыламасын алыңыз.
2. Шегерінділер әдісінің келесі параметрлері берілсін: а=403, с=0. Тізбек периоды Р=512 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 5 жаңа нақтыламасын алыңыз.
3. Шегерінділер әдісінің келесі параметрлері берілсін: а=101, с=2. Тізбек периоды Р=55 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 6 жаңа нақтыламасын алыңыз.
4. Шегерінділер әдісінің келесі параметрлері берілсін: а=0, с=152. Тізбек периоды Р=310 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 8 жаңа нақтыламасын алыңыз.
5. Шегерінділер әдісінің келесі параметрлері берілсін: а=45, с=20. Тізбек периоды Р=85 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 10 жаңа нақтыламасын алыңыз.
6. Шегерінділер әдісінің келесі параметрлері берілсін: а=255, с=125. Тізбек периоды Р=645 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 10 жаңа нақтыламасын алыңыз.
Практикалық сабақты өткізу түрі: жеке жоба жасау
Әдістемелік ұсыныс:
Бақылау мысалы 1. Шегерінділер әдісінің келесі параметрлері берілсін: а=397, с=199. Тізбек периоды Р=4 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 5 жаңа нақтыламасын алыңыз.
Шешуі:
Шегерінділер әдісінің толық алгоритмы көмегімен кездейсоқ сандар тізбегін модельдегенде, m-ге тең Р периодтың максималды ұзындығына келесі шарттар орындалғанда жетуге болады.
а) с және m - өзара жәй сандар;
б) а–1 саны 4-ке еселі, егер m саны да 4-ке еселі болса;
в) Z0*≤ m.
Олай болса Р = m = 4, Z0* ретінде 4-тен артық емес кез-келген санды алуға болады, мысалы Z0* = 3.
Сонымен а = 397, с = 199, Z0* = 3, m = 4.
Онда Z*n+1 = az*n+c(mod m) формуласы көмегімен базалық тізбектің 5 жаңа нақтыламасын табайық:
Z1* = 397 * 3 + 199 (mod 4) = 1390 (mod 4) = 2, Z1 = Z1* / m = 2/4 = 0,5
Z2* = 397 * 2 + 199 (mod 4) = 993 (mod 4) = 1, Z2 = Z2* / m = 1/4 = 0,25
Z3*= 397 * 1 + 199 (mod 4) = 596 (mod 4) = 0, Z3 = Z3* / m = 0/4 = 0
Z4*= 397 * 0 + 199 (mod 4) = 199 (mod 4) = 3, Z4 = Z4* / m = 3/4 = 0,75
Z5*= 397 * 3 + 199 (mod 4) = 1390 (mod 4) = 2, Z5 = Z5* / = m 2/4 = 0,5 және т.с.с
Бақылау мысалы 2. Шегерінділер әдісінің келесі параметрлері берілсін: а = 397, с = 0. Тізбек периоды Р = 2 шартын қанағаттандыратындай, басқа параметрлерді анықтаңыз, базалық тізбектің 3 жаңа нақтыламасын алыңыз.
Шешуі:
Шегерінділер әдісінің қысқартылған алгоритмі көмегімен кездейсоқ сандар тізбегін модельдегенде, m/4-ке тең Р периодтың максималды ұзындығына келесі шарттар орындалғанда жетуге болады:
а) Z0* кез-келген оң, тақ, бүтін сан;
б) а = 8t ± 3, мұндағы t – кез-келген оң, бүтін сан;
Р = m/4 = 2 болғандықтан, m = 4Р = 8, ал Z0* ретінде кез-келген тақ емес санды алуға болады, мысалы Z0* = 7.
Олай болса а = 397, с = 0, Z0* = 7, m =8.
Онда Z*n+1 = az*n(mod m) формуласы көмегімен базалық тізбектің 3 жаңа нақтыламасын табыңыз.
Z1* = 397 * 7 (mod 8) = 2779 (mod 8) = 3 Z1 = Z1* / m = 3/8 = 0,375
Z2* = 397 * 3 (mod 8) = 1191 (mod 8) = 7 Z2 = Z2* / m = 7/8 = 0,875
Z3* = 397 * 7 (mod 8) = 2779 (mod 8) = 3 Z3 = Z3* / m = 3/8 = 0,375 және т.с.с
Ұсынылған әдебиеттер: 1нег (8-17), 3нег (462-480), 6қос (10-25), 8қос (19-20)
